Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Chu vi, diện tích một số tứ giác SVIP
00:00
Ta kí hiệu C là chu vi, S là diện tích.
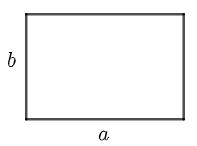
Hình chữ nhật |
| \(C=\left(a+b\right).2\) \(S=a.b\) |
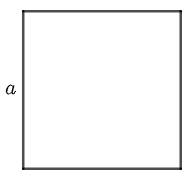
Hình vuông |
| \(C=a.4\) \(S=a.a\) |
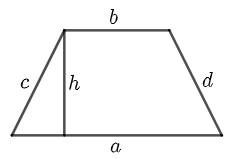
Hình thang |
| \(C=a+b+c+d\) \(S=\dfrac{\left(a+b\right).h}{2}\) |
Hình bình hành |
| \(S=a.h\) |
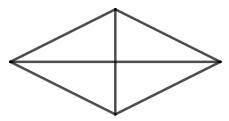
Hình thoi |
Độ dài hai đường chéo là $m$ và $n$. | \(S=\dfrac{m.n}{2}\) |
Ví dụ: Trên tường của phòng khách có treo một chiếc gương dạng hình thoi $ABCD$ như hình vẽ dưới. Tính diện tích chiếc gương đó biết mỗi ô vuông có cạnh là $2$ dm.
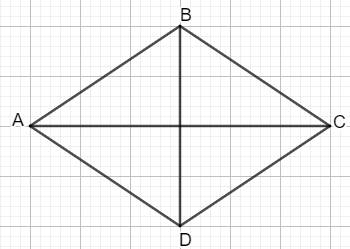
Giải
Chiếc gương dạng hình thoi có độ dài hai đường chéo là $12$ dm và $8$ dm, suy ra diện tích của nó là:
\(S=\dfrac{1}{2}.12.8=48\) (dm2).
Câu hỏi:
@200151228433@@200151231294@@200151273225@@200151366844@@200151532549@
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022