💯 Ôn tập và kiểm tra chương III

Câu 1 (1đ):

Cho tam giác $ABC$ có $AB = 16, CA = 21, \widehat{A} = 60^\circ$ . Độ dài cạnh $BC$ là

21

.

19

.

20

.

22

.

Câu 2 (1đ):

Cho $\sin x=\dfrac{1}{4},90^\circ< x< 180^\circ$ . Khẳng định nào sau đây đúng?

\cos x=\dfrac{\sqrt{15}}{4},\tan x=-\dfrac{1}{\sqrt{15}}

.

\cos x=-\dfrac{\sqrt{15}}{4},\tan x=\dfrac{1}{\sqrt{15}}

.

\cos x=\dfrac{\sqrt{15}}{4},\tan x=\dfrac{1}{\sqrt{15}}

.

\cos x=-\dfrac{\sqrt{15}}{4},\tan x=-\dfrac{1}{\sqrt{15}}

.

Câu 3 (1đ):

Giá trị biểu thức $P = \sin30^{\circ}\cos60^{\circ} + \sin60^{\circ}\cos30^{\circ}$ bằng

0.

- \sqrt{3}.

1.

\sqrt{3}.

Câu 4 (1đ):

Cho $\alpha$ và $\beta$ là hai góc khác nhau và bù nhau. Đẳng thức nào sau đây sai?

\cos\alpha = - \cos\beta.

\cot\alpha = \cot\beta.

\tan\alpha = - \tan\beta.

\sin\alpha = \sin\beta.

Câu 5 (1đ):

Để đo khoảng cách từ một điểm A trên bờ sông đến một cái cây cổ thụ (C) trên cù lao ở giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy nhau và nhìn thấy C, người ta đo được $AB = 50m$ , $\alpha =\widehat{CAB}=41^o$ , $\beta =\widehat{CBA}=66^o$ . Khoảng cách $AC$ gần nhất với giá trị nào sau đây?

35,9 m.

34,3 m.

69,6 m.

47,8 m.

Câu 6 (1đ):

Áp dụng công thức Hê rông để tính diện tích. Áp dụng công thức $S = \dfrac{abc}{4R} \Rightarrow R = \dfrac{abc}{4S}$ trong đó a, b, c là ba cạnh của tam giác và R là bán kính đường tròn ngoại tiếp.

Một tam giác có ba cạnh a = 3, b = 4, c = 5. Bán kính đường tròn ngoại tiếp R của tam giác bằng

4.

3.

4,5.

2,5.

Câu 7 (1đ):

Tam giác $ABC$ có $a = 21,b = 17,c = 10$ . Gọi $B'$ là hình chiếu vuông góc của $B$ trên cạnh $AC$ . Độ dài $BB'$ bằng

8

.

\dfrac{84}{5}

.

\dfrac{168}{17}

.

\dfrac{84}{17}

.

Câu 8 (1đ):

Tam giác $ABC$ có $\widehat{B}=60^{\circ}$ , $\widehat{C}=45^{\circ}$ , $AB=5$ . Độ dài cạnh $AC$ bằng

5\sqrt{3}

.

\dfrac{5\sqrt{6}}{2}

.

5\sqrt{2}

.

10

.

Câu 9 (1đ):

Tam giác $ABC$ vuông tại $A$ , đường cao $AH = 32\text{\ \ cm}$ . Hai cạnh $AB$ và $AC$ tỉ lệ với $3$ và $4$ . Cạnh nhỏ nhất của tam giác này có độ dài bằng

38\text{\ \ cm}.

40\text{\ \ cm}.

45\text{\ \ cm}.

42\text{\ \ cm}.

Câu 10 (1đ):

Tam giác đều $ABC$ có đường cao $AH$ . Khẳng định nào sau đây đúng?

\sin\widehat{ABC} = \dfrac{\sqrt{3}}{2}.

\sin\widehat{AHC} = \dfrac{1}{2}.

\cos\widehat{BAH} = \dfrac{1}{\sqrt{3}}.

\sin\widehat{BAH} = \dfrac{\sqrt{3}}{2}.

Câu 11 (1đ):

Giá trị biểu thức $P = \sin30{^\circ}\cos15{^\circ} + \sin150{^\circ}\cos165{^\circ}$ bằng

{0.}

{-}\dfrac{{3}}{{4}}{.}

\dfrac{{1}}{{2}}{.}

{1.}

Câu 12 (1đ):

Cho hai góc nhọn $\alpha$ và $\beta$ trong đó $\alpha < \beta$ . Khẳng định nào sau đây sai?

\tan\alpha + \tan\beta > 0.

\sin\alpha < \sin\beta.

\cos\alpha < \cos\beta.

\cot\alpha > \cot\beta.

Câu 13 (1đ):

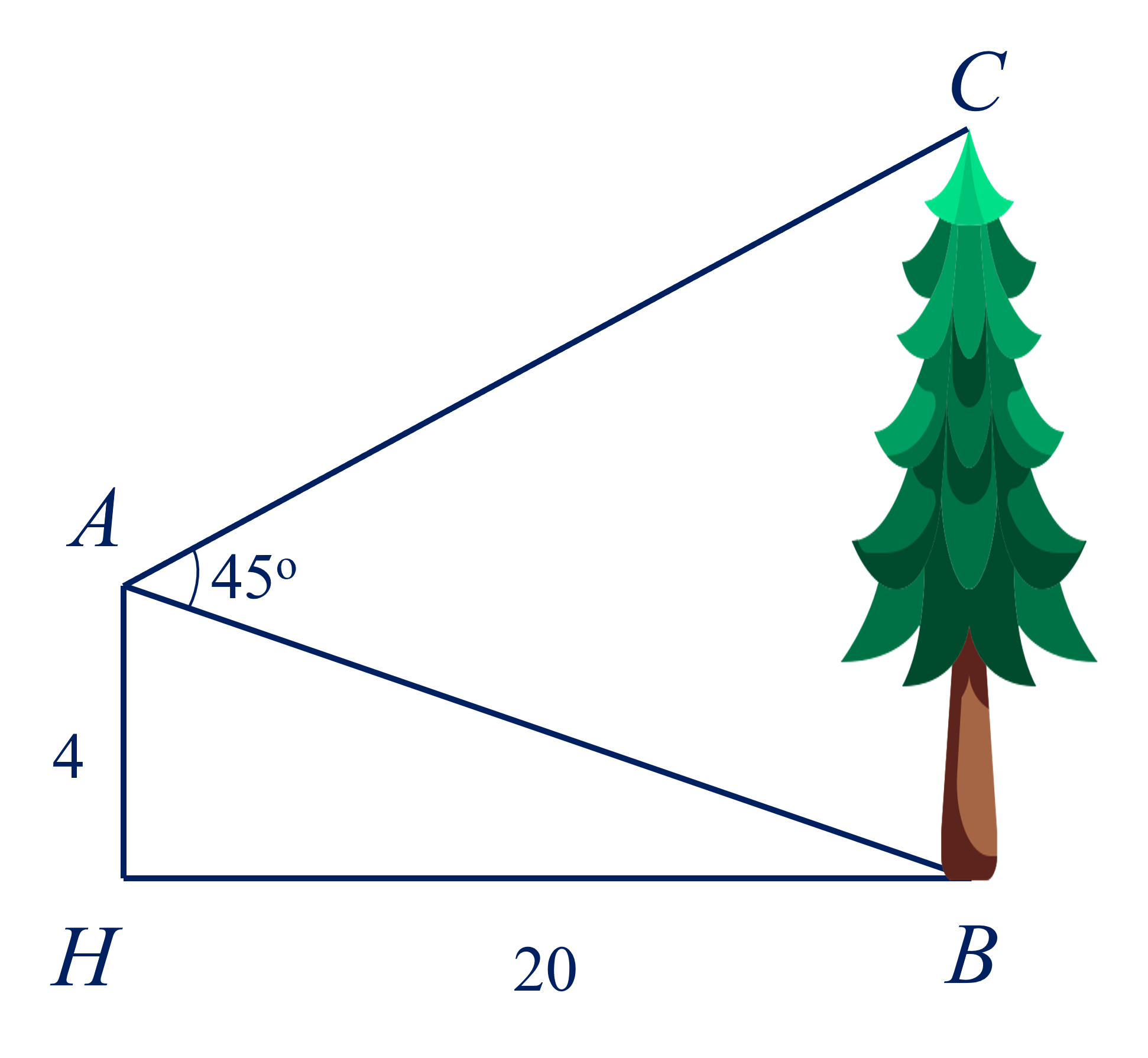
loading...

Từ vị trí $A$ người ta quan sát một cây cao (hình vẽ). Biết $AH \perp HB, \,AH = 4\ m,\ HB = 20\ m,\ \widehat{BAC} = 45^\circ$ . Chiều cao của cây gần nhất với giá trị nào dưới đây?

16\ m

.

18\ m

.

17\ m

.

15\ m

.

Câu 14 (1đ):

Tam giác $ABC$ có $AB = 3,AC = 6$ và $\widehat{A} = 60{^\circ}$ . Bán kính của đường tròn ngoại tiếp tam giác $ABC$ là

R = 3

.

R = \sqrt{3}

.

R = 3\sqrt{3}

.

R = 6

.

Câu 15 (1đ):

Tam giác $ABC$ có $BC = a,CA = b,AB = c$ và có diện tích $S$ . Nếu tăng cạnh $BC$ lên $2$ lần đồng thời tăng cạnh $AC$ lên $3$ lần và giữ nguyên độ lớn của góc $C$ thì khi đó diện tích của tam giác mới được tạo nên bằng

4S

.

6S

.

3S

.

2S

.

Câu 16 (1đ):

Cho tam giác $ABC$ vuông cân tại $A$ có $AB=AC=30$ cm. Hai đường trung tuyến $BF$ và $CE$ cắt nhau tại $G$ . Diện tích tam giác $GFC$ là

75

cm

^2

.

15\sqrt{105}

cm

^2

.

50\sqrt{2}

cm

^2

.

50

cm

^2

.

Câu 17 (1đ):

Chia cả tử và mẫu cho

\cos \alpha

.

Cho $\tan\alpha=4$ . Tính giá trị biểu thức $P=\dfrac{2 \sin \alpha -2 \cos \alpha }{-\sin \alpha +\cos \alpha }$ .

\dfrac{6}{5}

.

-\dfrac{10}{3}

.

-2

.

2

.

Câu 18 (1đ):

Cho tam giác $ABC$ . Giá trị biểu thức $P = \sin A\text{.cos}(B + C) + \cos A\text{.sin}(B + C)$ bằng

{-1.}

2.

{1.}

{0.}

Câu 19 (1đ):

Cho biết $\tan\alpha = - 3.$ Giá trị của $P = \dfrac{6\sin\alpha - 7\cos\alpha}{6\cos\alpha + 7\sin\alpha}$ bằng

\dfrac{{4}}{{3}}{.}

\dfrac{{5}}{{3}}{.}

{-}\dfrac{{4}}{{3}}{.}

{-}\dfrac{{5}}{{3}}{.}

Câu 20 (1đ):

Cho biết $\cos\alpha + \sin\alpha = \dfrac{1}{3}.$ Giá trị của $P = \sqrt{\tan^{2}\alpha + \cot^{2}\alpha}$ bằng

\dfrac{{11}}{{4}}{.}

\dfrac{{5}}{{4}}{.}

\dfrac{{7}}{{4}}{.}

\dfrac{{9}}{{4}}{.}

Câu 21 (1đ):

Tam giác $ABC$ có AB = c = 6cm, AC = b = 5cm, BC = a = 7cm. Độ dài đường trung tuyến $m_a$ ứng với cạnh BC bằng

\sqrt{7}

cm.

2\sqrt{7}

cm.

\dfrac{\sqrt{73}}{2}

cm.

\dfrac{\sqrt{145}}{2}

cm.

Câu 22 (1đ):

Tam giác $ABC$ có $AB = 4, BC = 6,$ $AC = 5$ . Điểm $M$ thuộc đoạn $BC$ sao cho $MC = 2MB$ .

Độ dài đoạn thẳng $AM$ bằng

\sqrt{11}

.

2\sqrt{2}

.

\sqrt{19}

.

2\sqrt{3}

.

Câu 23 (1đ):

Tam giác $ABC$ có $BC = 2\sqrt{3},AC = 2AB$ và độ dài đường cao $AH = 2$ . Độ dài cạnh $AB$ bằng

\dfrac{2\sqrt{3}}{3}

.

2

hoặc

\dfrac{2\sqrt{21}}{3}

.

2

hoặc

\dfrac{2\sqrt{3}}{3}

.

2

.

Câu 24 (1đ):

Tam giác $ABC$ có $AB = c,\ \ BC = a,\ \ CA = b$ . Các cạnh $a,\ b,\ c$ liên hệ với nhau bởi đẳng thức $b\left( b^{2} - a^{2} \right) = c\left( a^{2} - c^{2} \right)$ . Khi đó góc $\widehat{BAC}$ bằng

60{^\circ}.

30{^\circ}.

45{^\circ}.

90{^\circ}.

Câu 25 (1đ):

Bán kính đường tròn ngoại tiếp tam giác $ABC$ biết $AB=12$ và $\cot (A+B)=\dfrac{1}{3}$ bằng

\dfrac{9\sqrt{10}}{5}

.

5\sqrt{10}

.

2\sqrt{10}

.

3\sqrt{2}

.

Bài học cùng chủ đề

💯 Ôn tập và kiểm tra chương III SVIP

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

💯 Ôn tập và kiểm tra chương III SVIP

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP