Đề kiểm tra cuối học kì I - lớp 12 bộ sách Kết nối tri thức

Câu 1 (1đ):

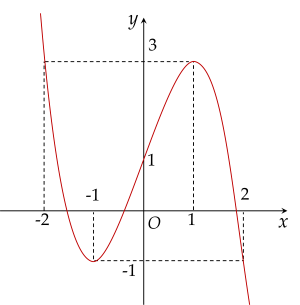
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ , có đồ thị như hình vẽ.

Mệnh đề nào sau đây đúng?

Hàm số nghịch trên trên

\mathbb{R}

.

Hàm số nghịch trên trên

(0;1)

.

Hàm số nghịch trên trên

(-\infty ;0)

.

Hàm số đồng biến trên

\mathbb{R}

.

Câu 2 (1đ):

Hàm số $y=x^3-3x^2+4$ đồng biến trên mỗi khoảng nào sau đây?

(-\infty ;1)

và

(2;+\infty)

.

(0;2)

.

(-\infty ;0)

và

(2;+\infty)

.

(0;1)

.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ dưới đây:

Cho hàm số $y=f(x) $ có bảng biến thiên như hình vẽ dưới đây

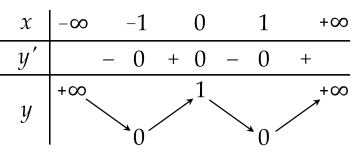
Giá trị cực đại của hàm số đã cho là

y=0

.

x=0

.

y=1

.

x=1

.

Câu 4 (1đ):

Đồ thị hàm số $y=\dfrac{5}{x-1}$ có tiệm cận ngang là đường thẳng nào dưới đây?

y=0

.

x=1

.

y=5

.

x=0

.

Câu 5 (1đ):

Cho tứ diện $ABCD$ . Gọi $G$ là trọng tâm tam giác $ABC.$ Giá trị của $k$ thích hợp điền vào đẳng thức vectơ $\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=k\overrightarrow{DG}$ là

k=\dfrac{1}{3}

.

k=\dfrac{1}{2}

.

k=2.

k=3.

Câu 6 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho hình chữ nhật $OKMN$ .

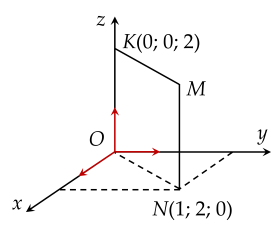
loading...

Tọa độ đỉnh $M$ của hình chữ nhật là

M\left( -1;-\,2;\,-2 \right)

.

M\left( 1;\,2;\,2 \right)

.

M\left( 0;\,2;\,2 \right)

.

M\left( 1;2;\,0 \right)

.

Câu 7 (1đ):

Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:

Tổng thu nhập (triệu đồng)	Số hộ gia đình
$[200;250)$	$0$
$[250;300)$	$45$
$[300;350)$	$34$
$[350;400)$	$21$
$[400;450)$	$0$

Khoảng biến thiên của mẫu số liệu trên là

100.

250.

150.

200.

Câu 8 (1đ):

Trong không gian với hệ tọa độ $O x y z$ , cho hai điểm $A(1 ; 2 ;-3)$ và $B(-3 ; 4 ; 5)$ . Tọa độ trung điểm $I$ của đoạn thẳng $A B$ là

I(-1 ; 3 ; 1).

I(2 ;-1 ;-4).

I(-1 ;-3 ; 1).

I(-2 ; 1 ; 4).

Câu 9 (1đ):

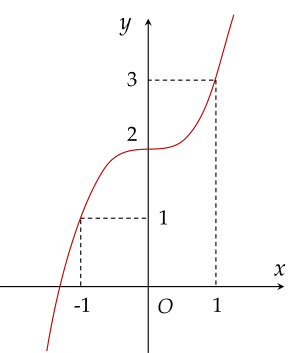
Cho hàm số $y=f\left(x \right)$ có đồ thị như hình vẽ.

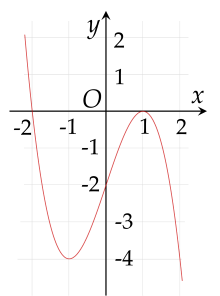
loading...

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

(-2;0)

.

(-1;1)

.

(1 ; 2)

.

(-2 ; 1)

.

Câu 10 (1đ):

Cho hàm số $y=-x^{3}+3 x+1$ có đồ thị là hình vẽ nào sau đây?

Câu 11 (1đ):

Giá trị của tham số $m$ để giá trị nhỏ nhất của hàm số $y=2 x^3-3 x^2+m$ trên đoạn $[0 ; 5]$ bằng $5$ là

m=3

.

m=2

.

m=-1

.

m=6

.

Câu 12 (1đ):

Trong không gian với hệ trục tọa độ $O x y z$ , cho tam giác $A B C$ có ba đỉnh $A(-1 ; 1 ;-3)$ , $B (4 ; 2 ; 1)$ , $C( 3 ; 0 ; 5)$ . Tọa độ trọng tâm $G$ của tam giác $A B C$ là

G (2 ; 1 ; 1).

G (3 ; 1 ; 1).

G (1 ; 3 ; 2).

G(-1 ; 2 ; 1).

Câu 13 (1đ):

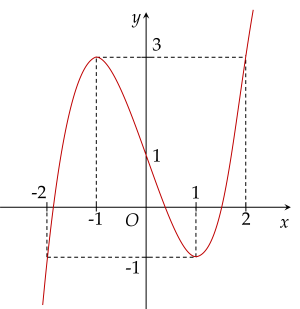
Cho hàm số $y=f(x)$ liên tục và có đồ thị trên đoạn $[-2 ; 4]$ như hình vẽ.

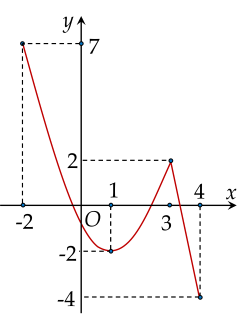
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Trên đoạn $[-2 ; 4]$ , đồ thị hàm số $y = f(x)$ có $2$ điểm cực trị.
b) Giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;2]$ là $-2$ .
c) Giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[1;4]$ là $-4$ .
d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;4]$ là $11$ .

Câu 14 (1đ):

Biểu đồ dưới đây mô tả kết quả điều tra về mức lương khởi điểm (đơn vị: triệu đồng) của một số công nhân ở hai khu vực $A$ và $B$ .

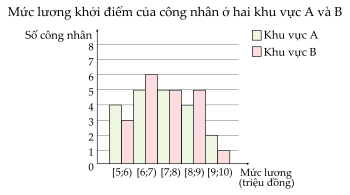
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hai khu vực $A$ và $B$ có mức lương trung bình bằng nhau.
b) Phương sai của mẫu số liệu ở khu vực $A$ lớn hơn $1,5.$
c) Độ lệch chuẩn của mẫu số liệu ở khu vực $B$ lớn hơn $1,2$ .
d) Mức lương khởi điểm của công nhân khu vực $B$ đồng đều hơn của công nhân khu vực $A$ .

Câu 15 (1đ):

Cho hình hộp $ABCD.A'B'C'D'$ . Gọi $I$ và $K$ lần lượt là tâm của hình bình hành $ABB'A'$ và $BCC'B'$ .

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{IK}=\dfrac{1}{2}\overrightarrow{AC}$ .
b) $\overrightarrow{IK}=\dfrac{1}{2}\overrightarrow{A'C'}$ .
c) $\overrightarrow{BD}+2\overrightarrow{IK}=\overrightarrow{BC}$ .
d) Ba vectơ $\overrightarrow{BD};\,\overrightarrow{IK};\,\overrightarrow{B'C'}$ không đồng phẳng.

Câu 16 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

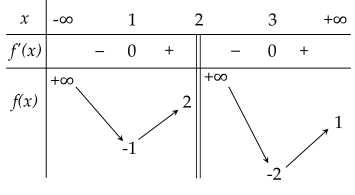
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giá trị nhỏ nhất của hàm số trên $[-2,5 ; 1,5]$ là $-2$ .
b) Hàm số xác định và liên tục trên $\mathbb{R}$ .
c) Điểm cực tiểu của đồ thị hàm số đã cho là $(3;-2)$ .
d) Với $-1\lt m\lt 1$ thì phương trình $f(x)=m$ có $4$ nghiệm phân biệt.

Câu 17 (1đ):

Một cốc chứa $20$ ml dung dịch KOH (Potassium Hydroxide) với nồng độ $100$ mg/ml và một bình chứa dung dịch KOH khác với nồng độ $10$ mg/ml. Lấy $x$ (ml) ở bình trộn vào cốc ta được dung dịch KOH có nồng độ $C(x)$ . Coi $C(x)$ là hàm số xác định với $x \geq 0$ . Khi $x \in[5 ; 15]$ , nồng độ của dung dịch KOH đạt giá trị lớn nhất bằng bao nhiêu mg/ml?

Trả lời: mg/ml

Câu 18 (1đ):

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $[-20 ; 20]$ để hàm số $y=x^4-2(m-1)x^2+m-2$ đồng biến trên khoảng $(1;3)$ ?

Trả lời:

Câu 19 (1đ):

Biết rằng với giá trị của tham số $m=\dfrac{a}{b}$ , với $a, \, b\in \mathbb{Z}, \, b>0$ , $\dfrac{a}{b}$ là phân số tối giản thì đồ thị hàm số $y=\dfrac{x+m+1}{x-1}$ là $(C_m)$ cắt đường thẳng $d: \, y=x+5$ tại hai điểm phân biệt $A, \, B$ sao cho $AB=10\sqrt{2}$ . Tính $P=a+b$ .

Trả lời:

Câu 20 (1đ):

Một chất điểm chuyển động theo quy luật và quãng đường di chuyển được sau $t$ giây được tính theo công thức $S\left(t \right)=-3t^3+243t^2$ (m). Vận tốc $v$ (m/s) của chuyển động đạt giá trị lớn nhất khi $t$ bằng bao nhiêu giây?

Trả lời:

Câu 21 (1đ):

Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc $100^\circ$ và có độ lớn lần lượt là $25$ N và $12$ N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn $4$ N. Tính độ lớn của hợp lực của ba lực trên. (làm tròn đến hàng đơn vị)

Trả lời:

Câu 22 (1đ):

Cho biểu đồ thống kê chiều cao của học sinh nữ lớp 12A:

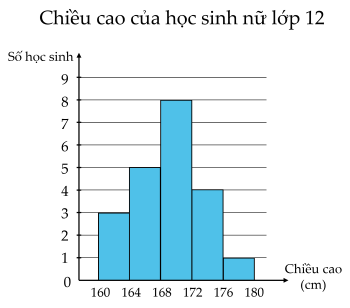
loading...

Tính độ lệch chuẩn của mẫu số liệu trên. (Làm tròn kết quả đến chữ số hàng phần trăm)

Trả lời: .

Bài học cùng chủ đề

Đề kiểm tra cuối học kì I - lớp 12 bộ sách Kết nối tri thức SVIP

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra cuối học kì I - lớp 12 bộ sách Kết nối tri thức SVIP

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP