Đề kiểm tra học kì I (đề số 2)

Câu 1 (1đ):

Mẫu số liệu sau ghi lại cân nặng (đơn vị: ki-lô-gam) của các bạn tổ II lớp 10A lần lượt là:

$\,\,\,\,\,38\,\,\,\,\,40\,\,\,\,\,55\,\,\,\,\,44\,\,\,\,\,\,50\,\,\,\,\,82\,\,\,\,\,78\,\,\,\,\,65\,\,\,\,\,48\,\,\,\,\,44\,\,\,\,\,\,54$ .

Trung vị của mẫu số liệu trên là

50

.

49

.

48

.

54

.

Câu 2 (1đ):

Cho giá trị gần đúng của $\dfrac{8}{17}$ là $0,47$ . Sai số tuyệt đối của số $0,47$ là giá trị nào sau đây?

0,001

.

0,002

.

0,003

.

0,004

.

Câu 3 (1đ):

Cho tam giác $ABC$ vuông tại $A$ , $G$ là trọng tâm tam giác $ABC,\, BC=a$ . Độ dài vectơ $\overrightarrow{AG}$ là

\dfrac{a}{6}

.

\dfrac{a}{3}

.

\dfrac{a\sqrt{3}}2

.

\dfrac{2a}{3}

.

Câu 4 (1đ):

Giá trị $\cos 45^\circ + \sin 45^\circ$ bằng

\sqrt{3}

.

0

.

1

.

\sqrt{2}

.

Câu 5 (1đ):

Parabol $y=x^2-4x+3$ có tọa độ đỉnh là

I(2;\,1 )

.

I(-2;\,1 )

.

I(-1;\,2 )

.

I(2;\,-1 )

.

Câu 6 (1đ):

Cho hàm số $y=-3x+5$ . Trong bốn điểm $A(-2;3)$ , $B(1;2)$ , $C(0;5)$ , $D(-1;2)$ , có bao nhiêu điểm thuộc đồ thị hàm số đã cho?

2

.

3

.

1

.

4

.

Câu 7 (1đ):

Cho $A=\left[-1;5 \right), \, B=\left(2;7 \right]$ . Tập $A \backslash B$ là

\left[-1;2 \right)

.

\left(2;5 \right)

.

\left[-1;2 \right]

.

\left[-1;7 \right]

.

Câu 8 (1đ):

Cho hai vectơ $\overrightarrow{a}$ ; $\overrightarrow{b}$ khác vectơ $\overrightarrow{0}$ thỏa mãn $\overrightarrow{a}.\overrightarrow{b}=\dfrac12\left| -\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|$ . Khi đó góc giữa hai vectơ $\overrightarrow{a}$ ; $\overrightarrow{b}$ bằng

150^\circ

.

120^\circ

.

60^\circ

.

30^\circ

.

Câu 9 (1đ):

Cho tam giác $ABC$ . Điểm $I$ trên cạnh $AC$ sao cho $CI=\dfrac14CA$ . Phân tích $\overrightarrow{BI}$ theo hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ ta được

\overrightarrow{BI}=\dfrac{1}{4}\overrightarrow{AC}-\overrightarrow{AB}

.

\overrightarrow{BI}=\dfrac{5}{4}\overrightarrow{AC}+\overrightarrow{AB}

.

\overrightarrow{BI}=\dfrac{3}{4}\overrightarrow{AC}-\overrightarrow{AB}

.

\overrightarrow{BI}=\dfrac{3}{4}\overrightarrow{AC}+\overrightarrow{AB}

.

Câu 10 (1đ):

Cho $A = \cos (90^\circ-x). \sin (180^\circ-x)$ . Khẳng định nào sau đây đúng?

A=\cos^2 x

.

A=-\sin x\cos x

.

A=\sin^2 x

.

A=\sin x\cos x

.

Câu 11 (1đ):

Giá trị nhỏ nhất của hàm số $y=5x^2+2x+1$ trên đoạn $[-2 ; 2]$ là

17

.

\dfrac{16}{5}

.

25

.

\dfrac{4}{5}

.

Câu 12 (1đ):

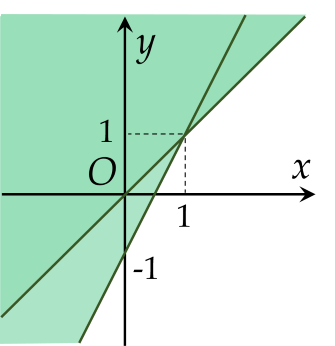
Phần không tô màu trong hình vẽ dưới đây (không tính biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?

loading...

\left\{ \begin{aligned} & x-y<0 \\ & 2x-y>1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x-y>0 \\ & 2x-y>1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x-y<0 \\ & 2x-y<1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x-y>0 \\ & 2x-y<1 \\ \end{aligned} \right.

.

Câu 13 (1đ):

Cuối học kì I vừa qua, bạn An đạt được kết quả sáu môn như sau:

Môn	Điểm trung bình
Toán	$7,2$
Văn	$8,0$
Anh	$5,8$
Lý	$7,2$
Hóa	$9,0$
Sinh	$4,6$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điểm trung bình các môn thi học kì của bạn An làm tròn đến hàng phần mười là $7,0$ .
b) Điểm trung bình các môn thi học kì của bạn An là $7,3$ .
c) Khoảng biến thiên của bảng điểm của bạn An bằng $3,4$ .
d) Khoảng tứ phân vị bảng điểm của bạn An bằng $2,2$ .

Câu 14 (1đ):

Cho tam giác $ABC$ vuông tại $A$ có $AB=a, \, BC=2a$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Tích vô hướng $\overrightarrow{AB}.\overrightarrow{AC}=0$ .
b) Góc giữa hai vectơ $\overrightarrow{BA}$ và $\overrightarrow{BC}$ bằng $30^\circ$ .
c) Tích vô hướng $\overrightarrow{BC}.\overrightarrow{AC}=3a^2$ .
d) Giá trị của biểu thức $\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{BC}.\overrightarrow{CA}+\overrightarrow{CA}.\overrightarrow{AB}=-4a^2$ .

Câu 15 (1đ):

Cho hàm số $y=(m^2-1)x+(m-1)$ với $m$ là tham số.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Với $m=3$ hàm số đồng biến trên $\mathbb{R}$ .
b) Với $m=-2$ đồ thị hàm số là đường thẳng đi lên từ trái qua phải.
c) Có ba giá trị nguyên của $m$ để hàm số nghịch biến trên $\mathbb{R}$ .
d) Hàm số đồng biến trên $\mathbb{R}$ khi $m\in (-\infty ;-1) \cup (1;+\infty)$ .

Câu 16 (1đ):

Cho hàm số $y=-x^2+6x-5$ có đồ thị $(P)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $y>0$ khi $x\in (1;5)$ .
b) $y\lt 0$ khi $x\in (-\infty ;1)\cup (5;+\infty)$ .
c) Giá trị lớn nhất của hàm số bằng $3$ .
d) Đường thẳng $d: \, y=4x-m$ cắt đồ thị $(P)$ tại hai điểm phân biệt khi $m>4$ .

Câu 17 (1đ):

Hai bạn An và Bình cùng di chuyển một xe đẩy trên đường phẳng bằng cách: bạn An đẩy xe từ phía sau theo hướng di chuyển của xe bằng một lực $F_1=2$ N, bạn Bình kéo xe từ phía trước theo hướng di chuyển của xe một lực $F_2=3$ N. Giả sử hai bạn thực hiện đúng kỹ thuật để xe di chuyển hiệu quả nhất. Xe di chuyển với lực tác động có độ lớn bằng bao nhiêu N?

Trả lời:

Câu 18 (1đ):

Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày:

$\,\,\,\,\,7\,\,\,\,\,8\,\,\,\,\,22\,\,\,\,\,20\,\,\,\,\,15\,\,\,\,\,18\,\,\,\,\,19\,\,\,\,\,13\,\,\,\,\,11$

Khoảng tứ phân vị cho mẫu số liệu này bằng bao nhiêu?

Trả lời:

Câu 19 (1đ):

Hai chiếc tàu thuỷ cùng xuất phát từ vị trí $A$ , đi thẳng theo hai hướng tạo với nhau một góc $60^\circ$ . Tàu thứ nhất chạy với tốc độ $30$ km/h, tàu thứ hai chạy với tốc độ $40$ km/h. Sau $2$ giờ hai tàu cách nhau bao nhiêu km? (làm tròn kết quả đến chữ số hàng phần mười)

Trả lời:

Câu 20 (1đ):

Một nhà trọ có giá $35$ phòng và có giá thuê là $2,5$ triệu đồng trên mỗi phòng thì khách thuê luôn kín phòng. Qua khảo sát thị trường thì thấy rằng nếu cứ tăng $100 \, 000$ đồng trên $1$ phòng thì có $1$ phòng trống. Tính số tiền trên mỗi phòng (đơn vị triệu đồng) để lợi nhuận mà chủ nhà nhận được lớn nhất. (làm tròn kết quả đến hàng đơn vị)

Trả lời:

Câu 21 (1đ):

Một hộ gia đình có ý định mua một cái máy bơm để phục vụ cho việc tưới tiêu vào mùa hạ. Khi đến cửa hàng thì được ông chủ giới thiệu về hai loại máy bơm có lưu lượng nước trong một giờ và chất lượng máy là như nhau.

Máy thứ nhất giá $1$ $500$ $000$ đồng và trong một giờ tiêu thụ hết $1,2$ kW.

Máy thứ hai giá $2$ $000$ $000$ đồng và trong một giờ tiêu thụ hết $1$ kW.

Chi phí trả cho hai máy sử dụng là như nhau sau khoảng thời gian $x_0$ là bao nhiêu giờ?

Trả lời:

Câu 22 (1đ):

Người ta định dùng hai loại nguyên liệu để chiết xuất ít nhất $120$ kg hóa chất A và $9$ kg hóa chất B. Từ mỗi tấn nguyên liệu loại I giá $4$ triệu đồng có thể chiết xuất được $20$ kg chất A và $0,6$ kg chất B. Từ mỗi tấn nguyên liệu loại II giá $3$ triệu đồng có thể chiết xuất được $10$ kg chất A và $1,5$ kg chất B. Cần phải dùng tổng bao nhiêu tấn nguyên liệu cả hai loại để chi phí mua nguyên liệu là ít nhất. Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá $10$ tấn nguyên liệu loại I và không quá $9$ tấn nguyên liệu loại II. (làm tròn đến chữ số hàng phần mười)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP