Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra học kì I (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Tập hợp tất cả các giá trị của tham số m để phương trình cos2x=m vô nghiệm là
Cho cấp số cộng (un) có u1=5, u12=38 thì công sai là
Khảo sát về thời gian (phút) đi từ nhà đến nơi làm việc của một số nhân viên trong một công ty như sau.
| Thời gian (phút) | Số nhân viên |
| [15;20) | 6 |
| [20;25) | 14 |
| [25;30) | 25 |
| [30;35) | 37 |
| [35;40) | 21 |
| [40;45) | 13 |
| [45;50) | 9 |
Khẳng định nào sau đây sai?
Quan sát một phần cầu thang như hình vẽ dưới đây:

Khẳng định nào sau đây đúng?
Nếu đường thẳng a cắt mặt phẳng chiếu (P) tại điểm A thì hình chiếu của a sẽ
Cho hình lập phương ABCD.A′B′C′D′. Các cạnh nào sau đây song song với mặt phẳng (AA′C′C)?
Giới hạn lim(2n−5n) bằng
Cho cấp số nhân (un) có {u2+u4=60u3+u5=180. Số hạng đầu của cấp số nhân là
x→5+limx2−6x+5∣10−2x∣ bằng
Cho hàm số y=f(x)={x2+xkhix≥13x+1khix<1. Giá trị x→1+limf(x) bằng
Cho A=x→−1limx+1x2−x−2 và B=x→0limx2(3x+1−1). Giá trị của biểu thức A−2B là
Cho hàm số y=f(x)=⎩⎨⎧x+1−23−xkhix=3mx+2khix=3. Hàm số liên tục tại điểm x=3 khi m bằng
Cho dãy số (un) biết un=n+22n+1,n∈N∗.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hai số hạng đầu của dãy là u1=1 và u2=35. |
|
| b) Dãy số (un) là một dãy số tăng. |
|
| c) Dãy số (un) bị chặn trên bởi 1733. |
|
| d) Dãy số (un) có duy nhất một số hạng nguyên. |
|
Cho mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm sau:
Nhóm | Tần số |
[0;2) | 3 |
[2;4) | 8 |
[4;6) | 12 |
[6;8) | 12 |
[8;10) | 4 |
| a) Cỡ mẫu của mẫu số liệu là n=38. |
|
| b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: Q1≈2,69. |
|
| c) Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:Q2≈5,42. |
|
| d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: Q3=7,04. |
|
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang cân (AD // BC). I là giao điểm của AB và DC. O là giao điểm của AC và BD. M,K lần lượt là trung điểm của SC và AD.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Ba điểm S,O,I thẳng hàng. |
|
| b) Ba điểm K,O,I thẳng hàng. |
|
| c) DM cắt mặt phẳng (SAB) tại J, khi đó S,J,I thẳng hàng. |
|
| d) Mặt phẳng (α) qua M cắt các cạnh SA,SB,SDlần lượt tại P,N,Q thì SO,MP,NQ đồng quy. |
|
Một bãi đỗ xe tính phí 60 000 đồng cho giờ đầu tiên (hoặc một phần của giờ đầu tiên) và thêm 40 000 đồng cho mỗi giờ (hoặc một phần của mỗi giờ) tiếp theo, tối đa là 200 000 đồng.
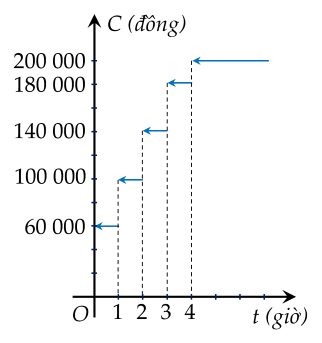
| a) Đồ thị hàm số C=C(t) trên biểu thị chi phí theo thời gian đỗ xe. |
|
| b) Hàm số C=C(t) liên tục trên [0;+∞). |
|
| c) Từ đồ thị ta thấy t→3limC(t)=180000. |
|
| d) Một người có thời gian đỗ xe tăng dần đến 3 giờ và một người có thời gian đỗ xe giảm dần đến 3 giờ thì chênh lệch chi phí giữa hai người là 20 000 đồng. |
|
Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m, thời gian thực hiện mỗi vòng quay của đu quay là 30 phút.
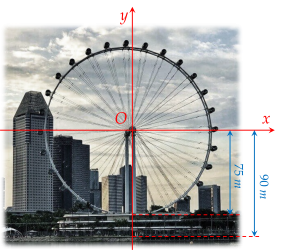
Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét? (làm tròn kết quả tới hàng phần mười)
Trả lời:
Trong thời gian liên tục 25 năm, một người lao động luôn gửi đúng 4000000 đồng vào một ngày cố định của tháng ở ngân hàng M với lãi suất không thay đổi trong suốt thời gian gửi tiền là 0,6% tháng. Gọi A đồng là số tiền người đó có được sau 25 năm. Tính A, đơn vị triệu đồng, làm tròn tới hàng đơn vị.
Trả lời:
Khảo sát số lần sử dụng Facebook của một người thực hiện mỗi ngày trong 30 ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:
| Số lần sử dụng facebook | Số ngày |
| [3;5] | 2 |
| [6;8] | 5 |
| [9;11] | 11 |
| [12;14] | 8 |
| [15;17] | 4 |
Tìm mốt của mẫu số liệu ghép nhóm trên?
Trả lời:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB, I là trung điểm của AB và M là điểm trên cạnh AD. Biết rằng đường thẳng MG song song với một mặt phẳng (SCD). Tỉ số giữa hai đoạn thẳng AM và AD là bao nhiêu (làm tròn đến hàng phần trăm)?
Trả lời:
Tìm tất cả các giá trị nguyên của tham số m trong [−2;9] sao cho phương trình (m2−5m+4)x5+x2+4=0 có nghiệm.
Trả lời:
Một vật có nhiệt độ 20∘C được nung nóng trong 70 phút rồi lại hạ nhiệt trong 50 phút tiếp theo. Biết rằng trong 70 phút đầu tiên, mỗi phút nhiệt độ của vật tăng 4∘C. Trong 50 phút kế tiếp, mỗi phút nhiệt độ của vật lại giảm 2∘C. Hàm số biểu thị nhiệt độ (∘C) của vật theo thời gian t (phút) có dạng: T(t)={20+4tkhi0≤t≤70a−2tkhi70<t≤120 (với a là hằng số). Biết rằng, y=T(t) là hàm liên tục trên tập xác định. Giá trị của a bằng bao nhiêu?
Trả lời:
