Đề kiểm tra học kì I (đề số 3)

Câu 1 (1đ):

Mệnh đề nào sau đây đúng?

A

Không có mặt phẳng nào chứa hai đường thẳng

a

và

b

thì ta nói

a

và

b

chéo nhau.

B

Hai đường thẳng song song nhau nếu chúng không có điểm chung.

C

Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.

D

Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau.

Câu 2 (1đ):

Cho tứ diện $ABCD$ . Trên các cạnh $AB$ và $AC$ lần lượt lấy các điểm $M$ và $N$ sao cho $\dfrac{AM}{AB}=\dfrac{AN}{AC}$ . Giao tuyến của hai mặt phẳng $(DBC)$ và $(DMN)$ là

A

Đường thẳng

DJ

với J là giao điểm của

MC

và

BN

.

B

Đường thẳng

DA

.

C

Đường thẳng qua

D

và song song với

MN

.

D

Đường thẳng qua

D

và song song với

MB

.

Câu 3 (1đ):

Cho cấp số nhân $(u{{}_{n}})$ biết $u_3=9$ và công bội $q=-3$ . Tổng ${{S}_{3}}$ của $3$ số hạng đầu của cấp số nhân $(u_n)$ bằng

1

.

7.

-14.

36.

Câu 4 (1đ):

$I=\lim \dfrac{7n^2-2n^3+1}{3n^3+2n^2+1}$ bằng

\dfrac{7}{3}

.

-\dfrac{2}{3}

.

1

.

0

.

Câu 5 (1đ):

Giá trị của $\underset{x \to 2}{\mathop{\lim}}(2x^2+3x-1)$ bằng

+\infty

.

13

.

11

.

14

.

Câu 6 (1đ):

Trong các hàm số sau, hàm số nào liên tục trên $\mathbb{R}$ ?

y=\sqrt{x^2-1}

.

y=\dfrac{2x-1}{x-1}

.

y=\cot x

.

y=x^3-x

.

Câu 7 (1đ):

Cho hình hộp $ABCD.A'B'C'D'$ . Khẳng định nào dưới đây đúng?

A

ABCD

là hình chữ nhật.

B

Các mặt bên của hình hộp là hình chữ nhật.

C

Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.

D

Các cạnh của hình hộp bằng nhau.

Câu 8 (1đ):

Tập xác định của hàm số $y=\tan x+\cot x$ là

\mathbb{R}\backslash \left\{ k\dfrac{\pi }{2} \, \big| \, k\in \mathbb{Z} \right\}

.

\mathbb{R}\backslash \left\{ k\pi \, \big| \, k\in \mathbb{Z} \right\}

.

\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi \, \big| \, k\in \mathbb{Z} \right\}

.

\mathbb{R}

.

Câu 9 (1đ):

Cho biết $\cot x=\dfrac12$ . Giá trị biểu thức $A=\dfrac2{\sin^2 x-\sin x\cos x-\cos^2 x}$ bằng

10

.

6

.

12

.

8

.

Câu 10 (1đ):

Cho cấp số cộng $(u_n)$ với $u_n=10-2n$ . Công sai của cấp số cộng bằng

-2

.

1

.

3

.

2

.

Câu 11 (1đ):

Giới hạn $I=\underset{x \to +\infty }{\mathop{\lim}}(x+1-\sqrt{x^2-x+2})$ bằng

\dfrac12

.

\dfrac{46}{31}

.

\dfrac32

.

\dfrac{17}{11}

.

Câu 12 (1đ):

Các giá trị của $m$ để hàm số $y = f(x)=\left\{ \begin{aligned} \dfrac{\sqrt{1-x}-\sqrt{1+x}}{x} \, \, khi \, \, x\lt 0 \\ m+\dfrac{1-x}{1+x} \, \, khi \, \, x \ge 0 \\ \end{aligned} \right.$ liên tục tại $x=0$ là

m=0

.

m=-1

.

m=-2

.

m=1

.

Câu 13 (1đ):

Cho tứ giác $ABCD$ có $AC$ và $BD$ giao nhau tại $O$ và một điểm $S$ không thuộc mặt phẳng $(ABCD)$ . Trên đoạn $SC$ lấy một điểm $M$ không trùng với $S$ và $C$ , $K=AM\cap SO$ .

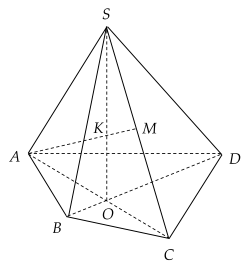
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $SO$ là giao tuyến của hai mặt phẳng $(SAC )$ , $(ABC)$ .
b) $SO$ là giao tuyến của hai mặt phẳng $(SAC )$ , $(SBD)$ .
c) Giao điểm của đường thẳng $SO$ với mặt phẳng $(ABM)$ là điểm $K$ .
d) Giao điểm của đường thẳng $SD$ với mặt phẳng $(ABM)$ là điểm $N$ thuộc đường thẳng $AK$ .

Câu 14 (1đ):

Biết giới hạn $\lim \dfrac{2n+1}{-3n+2}=a$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giá trị $a$ lớn hơn $0$ .
b) Ba số $-\dfrac{5}{3}; \, a; \, \dfrac{1}{3}$ tạo thành một cấp số cộng với công sai bằng $2$ .
c) Trên khoảng $\left(-\pi ;\pi \right)$ phương trình lượng giác $\sin x=a$ có $3$ nghiệm.
d) Cho cấp số nhân $(u_n)$ với công bội $q=3$ và $u_1=a$ thì $u_3=-6$ .

Câu 15 (1đ):

Cho phương trình $\sin^2\Big(2x+\dfrac{\pi }{4} \Big)=\cos^2\Big(x+\dfrac{\pi }{2} \Big)$ (*).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hạ bậc hai vế của (*), ta được phương trình: $\dfrac{1+\cos \Big(4x+\dfrac{\pi }{2} \Big)}{2}=\dfrac{1-\cos \Big(2x+\pi \Big)}{2}$ .
b) Ta có $\cos \Big(2x+\pi \Big)=-\cos 2x$ .
c) Phương trình đã cho đưa về dạng: $\cos \Big(4x+\dfrac{\pi }{2} \Big)=\cos 2x$ .
d) Nghiệm của phương trình (*) là $x=-\dfrac{\pi }{4}+k\pi$ và $x=\dfrac{\pi }{12}+k\dfrac{\pi }{3}, \, (k \in \mathbb{Z})$ .

Câu 16 (1đ):

Do nhu cầu đi lại của gia đình, anh Bình quyết định thực hiện tích góp tiền để mua một chiếc ôtô Vinfast VF8 trị giá $1,259$ tỉ đồng.

Đợt thứ nhất: anh Bình đã tích góp theo nguyên tắc tháng sau tích góp nhiều hơn tháng ngay trước đó số tiền là $2$ triệu đồng và cứ như thế đến tháng thứ $10$ anh phải góp $21$ triệu đồng. Đến hết đợt thứ nhất anh Bình có tất cả $624$ triệu đồng.

Đợt thứ hai kế tiếp: do muốn rút ngắn thời gian mua xe thì số tiền còn lại anh tiếp tục tích góp với tháng đầu là $5$ triệu đồng và mỗi tháng tiếp theo số tiền gấp đôi tháng kề trước nó.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đợt thứ nhất anh Bình tích lũy tiền theo dãy số là cấp số cộng có công sai là $d=2$ triệu đồng và $u_1=3$ triệu đồng.
b) Anh Bình tích lũy tiền hết đợt thứ nhất trong $25$ tháng.
c) Đợt thứ hai anh Bình tích lũy tiền theo dãy số là cấp số nhân có công bội là $q=2$ triệu đồng và $u_1=5$ triệu đồng.
d) Để đủ tiền mua ôtô thì anh Bình tích góp ít nhất $31$ tháng.

Câu 17 (1đ):

Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật $ABCD.EFGH$ là hình chiếu của thùng hàng đó lên mặt đất với phương chiếu $GM$ song song với các tia sáng mặt trời (các tia sáng mặt trời được xem là các đường thẳng song song với nhau), $M$ trùng với điểm đối xứng với $A$ qua $D$ . Tính diện tích phần bóng râm được tô màu trong hình vẽ bên dưới, biết rằng $BC=8$ m, $CD=2$ m và $CG=4$ m. (kết quả tính theo đơn vị m $^2$ )

Vào một thời điểm trong ngày, người ta quan sát thấy bóng râm của một thùng hàng dạng hình hộp chữ nhật

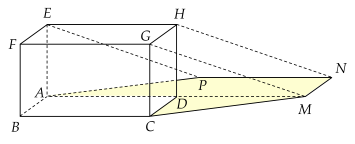
Trả lời:

Câu 18 (1đ):

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A,$ $\widehat{ABC}=60^\circ,$ $AB=8.$ Gọi $O, \, M$ lần lượt là trung điểm của $BC,AB.$ Mặt phẳng $(\alpha)$ qua $M$ và song song với $SB$ và $OA,$ cắt $BC, \, SC, \, SA$ lần lượt tại $N, \, P, \, Q.$ Tính diện tích của tứ giác $MNPQ$ , biết $SB \perp OA$ và $SB=8.$

Trả lời:

Câu 19 (1đ):

Cho số thực $a$ , $b$ , $c$ thỏa mãn $\left\{ \begin{aligned} & -8+4a-2b+c>0 \\ & 8+4a+2b+c\lt 0 \\ \end{aligned} \right.$ . Có bao nhiêu giao điểm của đồ thị hàm số $y=x^3+ax^2+bx+c$ và trục $Ox$ ?

Trả lời:

Câu 20 (1đ):

Giới hạn $\underset{x \to +\infty }{\mathop{\lim}} \Big(\sqrt{x^2-x}-\sqrt[3]{x^3+1}\Big)$ bằng bao nhiêu? (làm tròn đến chữ số hàng phần mười)

Trả lời:

Câu 21 (1đ):

Cho dãy số $(u_n )$ biết $\left\{ \begin{aligned}&u_1=1; \, u_2=2 \\&u_{n+2}=au_{n+1}+(1-a)u_n, \, \forall n \in \mathbb{N}^*\\ \end{aligned} \right.$ . Tìm giá trị nguyên nhỏ nhất của $a$ để dãy số $(u_n )$ tăng.

Trả lời:

Câu 22 (1đ):

Một rạp hát có $18$ hàng ghế cho khán giả được xếp theo hình quạt. Hàng thứ nhất có $16$ ghế, hàng thứ hai có $20$ ghế, hàng thứ ba có $24$ ghế,… cứ thế cho đến hàng cuối cùng. Trong một buổi hoà nhạc, ban tổ chức đã bán hết sạch vé và số tiền thu được chỉ từ việc bán vé là $135$ triệu đồng. Giá tiền mỗi tấm vé là bao nhiêu nghìn đồng, biết rằng các tấm vé đồng giá và số vé bán ra bằng số ghế trong rạp hát.

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP