olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Tải ma trận

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Cho hai góc nhọn aa và bb với tan⁡a=17\tan a=\dfrac{1}{7} và tan⁡b=34\tan b=\dfrac{3}{4}. Tổng a+ba+b bằng

π6.\dfrac{\pi }{6}.
π4.\dfrac{\pi }{4}.
π3.\dfrac{\pi }{3}.
2π3.\dfrac{2\pi }{3}.
Câu 2 (1đ):

Tập giá trị của hàm số y=sin⁡2xy=\sin 2x là

[−1;1]\left[ -1;1 \right].
[0;2]\left[ 0;2 \right].
[−2;2]\left[ -2;2 \right].
R\mathbb{R}.
Câu 3 (1đ):

Chu kì tuần hoàn TT của hàm số y=2 018tan⁡x+2 019y=2\, 018\tan x+2\, 019 là

T=2πT=2\pi .
T=4πT=4\pi
T=kπ, k∈ZT=k\pi, \, k\in \mathbb{Z}.
T=πT=\pi .
Câu 4 (1đ):

Nghiệm của phương trình tan⁡x=−1\tan x=-1 là

x=π4+kπ, k∈Zx=\dfrac{\pi }{4}+k\pi,\,k\in \mathbb{Z}.
x=π2+kπ, k∈Zx=\dfrac{\pi }{2}+k\pi, \,k\in \mathbb{Z}.
x=−π2+kπ, k∈Zx=\dfrac{-\pi }{2}+k\pi,\,k\in \mathbb{Z}.
x=−π4+kπ, k∈Zx=\dfrac{-\pi }{4}+k\pi, \,k\in \mathbb{Z}.
Câu 5 (1đ):

Cho cấp số cộng (un)(u_n) với un=5−2nu_n=5-2n. Công sai của cấp số cộng đó là

d=−2d=-2.
d=1d=1.
d=3d=3.
d=2d=2.
Câu 6 (1đ):

Cho dãy số (un)(u_n) được xác định bởi {u1=−2un=3un−1−1, ∀n≥2\left\{ \begin{aligned} & u_1=-2 \\ & u_n=3u_{n-1}-1,\, \forall n\ge 2 \\ \end{aligned} \right.. Số hạng u4u_4 là

−76-76.
−67-67.
−77-77.
−66-66.
Câu 7 (1đ):

Cho cấp số cộng (un) (u_n) có số hạng đầu bằng 2, 2, công sai bằng −3. -3. Tổng 99 99 số hạng đầu của cấp số cộng đã cho bằng

14 355. 14 \, 355.
−14 454. -14 \, 454.
−29 0072. -\dfrac{29 \, 007}{2}.
−14 355. -14 \, 355.
Câu 8 (1đ):

Cho dãy số có các số hạng đầu là 13; 132; 133; 134;... \dfrac13; \, \dfrac{1}{3^2}; \, \dfrac{1}{3^3}; \, \dfrac{1}{3^4};... . Số hạng tổng quát của dãy số này là

13n−1 \dfrac{1}{3^{n-1}}
13n \dfrac{1}{3^{n}} .
13n+1 \dfrac{1}{3^{n+1}} .
13n+2 \dfrac{1}{3^{n+2}} .
Câu 9 (1đ):

Cho sin⁡a=13\sin a=\dfrac{1}{3}. Giá trị của biểu thức A=cot⁡a−tan⁡atan⁡a+2cot⁡aA=\dfrac{\cot a-\tan a}{\tan a+2\cot a} bằng

717\dfrac{7}{17}.
1781\dfrac{17}{81}.
19\dfrac{1}{9}.
79\dfrac{7}{9}.
Câu 10 (1đ):

Giá trị lớn nhất của hàm số y=3sin⁡xy=3\sin x là

33.
−3-3.
22.
11.
Câu 11 (1đ):

Trong các dãy số có công thức tổng quát sau, dãy số nào là cấp số cộng?

un=n2−2u_n=n^2-2.
un=2 021nu_n=2 \, 021^n.
un=2n+2 021u_n=2n+2 \, 021.
un=2n+2 021u_n=\dfrac{2}{n+2 \, 021}.
Câu 12 (1đ):

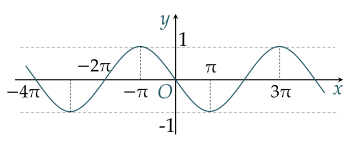
Đường cong trong hình vẽ là đồ thị của một trong bốn hàm số nào sau đây?

loading...

y=cos⁡x2y=\cos \dfrac{x}{2}.
y=−cos⁡x4y=-\cos \dfrac{x}{4}.
y=sin⁡x2y=\sin \dfrac{x}{2}.
y=sin⁡(−x2)y=\sin \Big(-\dfrac{x}{2} \Big).
Câu 13 (1đ):

Cho hàm số f(x)=sin⁡2x+cos⁡x−1f(x)=\sin^2 x+\cos x-1.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Tập xác định của hàm số D=RD=\mathbb{R}.
b) f(−π)=−f(π)f(-\pi)=-f(\pi).
c) f(−x)=f(x)f(-x)=f(x).
d) Hàm số đã cho là hàm số chẵn.
Câu 14 (1đ):

Cho phương trình lượng giác 2sin⁡x=22\sin x=\sqrt{2}.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Phương trình tương đương sin⁡x=sin⁡π4\sin x=\sin \dfrac{\pi }{4}.
b) Phương trình có nghiệm là: x=π3+k2π; x=3π4+k2π, (k∈Z)x=\dfrac{\pi }{3}+k2\pi ; \, x=\dfrac{3\pi }{4}+k2\pi, \, (k \in \mathbb{Z}).
c) Phương trình có nghiệm dương nhỏ nhất bằng π4\dfrac{\pi }{4}.
d) Số nghiệm của phương trình trong khoảng (−π2;π2)\Big(-\dfrac{\pi }{2};\dfrac{\pi }{2}\Big) là hai nghiệm.
Câu 15 (1đ):

Khi kí kết hợp đồng lao động với người lao động, một doanh nghiệp đề xuất hai phương án trả lương như sau:

Phương án 1: Năm thứ nhất, tiền lương là 120 120 triệu đồng. Kể từ năm thứ hai trở đi, mỗi năm tiền lương được tăng 18 18 triệu đồng.

Phương án 2: Quý thứ nhất, tiền lương là 24 24 triệu đồng. Kể từ quý thứ hai trở đi, mỗi quý tiền lương được tăng 1,8 1,8 triệu đồng.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Trong phương án 1: dãy số tiền lương là cấp số cộng có số hạng đầu tiên là u1=120 u_1=120 , công sai d1=18 {{d}_{1}}=18 .
b) Trong phương án 1: tiền lương người lao động nhận được trong năm thứ ba là 174 174 triệu đồng.
c) Trong phương án 1: tổng tiền lương người lao động nhận được trong ba năm là 414 triệu đồng.
d) Nếu kí hợp đồng lao động trong ba năm, với mong muốn nhận được tổng số tiền lương cao nhất thì người lao động nên chọn phương án 1.
Câu 16 (1đ):

Cho hàm số f(x)=∣x∣sin⁡xf(x)=|x|\sin x.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Tập xác định của hàm số là D=R\{0}D=\mathbb{R}\backslash \left\{ 0 \right\}.
b) f(−π)+f(π)=0f(-\pi)+f(\pi) = 0.
c) f(−x)=−f(x)f(-x)=-f(x).
d) Hàm số đã cho đối xứng qua gốc tọa độ O(0;0)O\left(0;0 \right).
Câu 17 (1đ):

Cho dãy số (un)(u_n) biết un=an+5n+2u_n=\dfrac{an+5}{n+2}. Có bao nhiêu giá trị nguyên của aa nhỏ hơn 100100 để dãy số (un)(u_n) là dãy số tăng.

Trả lời:

Câu 18 (1đ):

Trong một thí nghiệm, một viên bi sắt được gắn vào một đầu lò xo đàn hồi, đầu còn lại được cố định vào một thanh treo ngang. Sau khi viên bi được kéo xuống và thả ra, nó bắt đầu di chuyển lên xuống. Khi đó, chiều cao hh cm của bi so với mặt đất theo thời gian tt giây được cho bởi công thức: h=100−30cos⁡20t.h=100-30\cos 20t. Tính thời điểm đầu tiên mà bi sắt đạt chiều cao cao nhất kể từ khi nó được thả ra (làm tròn kết quả đến hàng phần trăm).

Trả lời:

Câu 19 (1đ):

Ông Sơn trồng cây trên một mảnh đất hình tam giác theo quy luật: ở hàng thứ nhất có 11 cây, hàng thứ hai có 22 cây, hàng thứ ba có 33 cây…, ở hàng thứ nn có nn cây. Biết rằng ông đã trồng hết 11 32511 \, 325 cây. Số hàng cây được trồng theo cách trên là bao nhiêu?

Trả lời:

Câu 20 (1đ):

Nguời ta thiết kế một cái tháp gồm 1010 tầng theo cách: Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng 11 bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là 12 28812 \, 288 m2^2, tính diện tích bề mặt trên cùng của tháp (đơn vị mét vuông).

Trả lời:

Câu 21 (1đ):

Gọi M, N, PM, \, N, \, P là các điểm trên đường tròn lượng giác sao cho số đo các góc lượng giác (OA,OM), (OA,ON), (OA,OP)(OA,OM), \, (OA,ON), \, (OA,OP) lần lượt bằng π2, 7π6, −π6\dfrac{\pi }{2}, \, \dfrac{7\pi }{6}, \, -\dfrac{\pi }{6}. Số đo góc lớn nhất của tam giác MNPMNP bằng bao nhiêu độ?

Trả lời:

Câu 22 (1đ):

Cho hình vuông A1B1C1D1 A_1B_1C_1D_1 có cạnh bằng 4 4 . Với mọi số nguyên dương n≥2 n \ge 2 , gọi An, Bn, Cn, Dn A_n, \, B_n, \, C_n, \, D_n lần lượt là trung điểm của các cạnh An−1Bn−1, Bn−1Cn−1, Cn−1Dn−1 A_{n-1}B_{n-1}, \, B_{n-1}C_{n-1}, \, C_{n-1}D_{n-1} , Dn−1An−1 D_{n-1}A_{n-1} . Gọi Sn S_n là diện tích của tứ giác AnBnCnDn A_n B_nC_nD_n . Tính 1S9 \dfrac{1}{S_9} .

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP