olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Thông tin của bạn

Ôn tập và kiểm tra chương Hàm số và phương trình lượng giác SVIP

Tải ma trận

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Giá trị biểu thức A=cos⁡(3π−a)+sin⁡(a−3π)−cos⁡(a−3π2)−sin⁡(3π2+a)A=\cos \left(3\pi -a \right)+\sin \left(a-3\pi \right)-\cos \Big(a-\dfrac{3\pi }{2}\Big)-\sin \Big(\dfrac{3\pi }{2}+a\Big) bằng

−1-1.
00.
11.
44.
Câu 2 (1đ):

Nếu sin⁡α=45\sin \alpha =\dfrac{4}{5} thì giá trị của cos⁡4α\cos 4\alpha là

−527625-\dfrac{527}{625}.
524625\dfrac{524}{625}.
−524625-\dfrac{524}{625}.
527625\dfrac{527}{625}.
Câu 3 (1đ):

Cho 2π<α<5π22\pi \lt \alpha \lt \dfrac{5\pi }{2}, kết quả nào sau đây đúng?

tan⁡α<0;cot⁡α>0\tan \alpha \lt 0;\cot \alpha >0.
tan⁡α<0;cot⁡α<0\tan \alpha \lt 0;\cot \alpha \lt 0.
tan⁡α>0;cot⁡α>0\tan \alpha >0;\cot \alpha >0.
tan⁡α>0;cot⁡α<0\tan \alpha >0;\cot \alpha \lt 0.
Câu 4 (1đ):

Hàm số nào dưới đây có đồ thị là đường cong như hình vẽ?

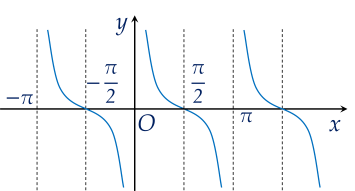
loading...

y=cot⁡xy=\cot x.
y=tan⁡xy=\tan x.
y=cos⁡xy=\cos x.
y=sin⁡xy=\sin x.
Câu 5 (1đ):

Mệnh đề nào sau đây sai?

y=sin⁡xy=\sin x tuần hoàn với chu kì 2π2\pi .
y=cot⁡xy=\cot x tuần hoàn với chu kì π\pi .
y=cos⁡xy=\cos x tuần hoàn với chu kì 2π2\pi .
y=tan⁡xy=\tan x tuần hoàn với chu kì 2π2\pi .
Câu 6 (1đ):

Nghiệm của phương trình sin⁡(2x+π3)=32\sin \Big(2x+\dfrac{\pi }{3} \Big)=\dfrac{\sqrt{3}}{2} là

[x=kπx=π6+kπ, ( k∈Z)\left[ \begin{aligned} & x=k\pi \\ & x=\dfrac{\pi }{6}+k\pi \\ \end{aligned} \right., \, \left(\, k\in \mathbb{Z} \right).
[x=kπx=−π3+kπ, ( k∈Z)\left[ \begin{aligned} & x=k\pi \\ & x=-\dfrac{\pi }{3}+k\pi \\ \end{aligned} \right., \, \left(\, k\in \mathbb{Z} \right).
[x=k2πx=π3+k2π, ( k∈Z)\left[ \begin{aligned} & x=k2\pi \\ & x=\dfrac{\pi }{3}+k2\pi \\ \end{aligned} \right., \, \left(\, k\in \mathbb{Z} \right).
[x=−π12+kπx=π4+kπ, ( k∈Z)\left[ \begin{aligned} & x=-\dfrac{\pi }{12}+k\pi \\ & x=\dfrac{\pi }{4}+k\pi \\ \end{aligned} \right., \, \left(\, k\in \mathbb{Z} \right).
Câu 7 (1đ):

Nghiệm của phương trình tan⁡x=1\tan x=1 là

x=kπ, k∈Zx=k\pi,\,k\in \mathbb{Z}.
x=π4+k2π, k∈Zx=\dfrac{\pi }{4}+k2\pi,\, k\in \mathbb{Z}.
x=k2π, k∈Zx=k2\pi,\,k\in \mathbb{Z}.
x=π4+kπ, k∈Zx=\dfrac{\pi }{4}+k\pi,\,k\in \mathbb{Z}.
Câu 8 (1đ):

Cho cot⁡a=15\cot a=15, giá trị sin⁡2a\sin 2a nhận giá trị nào dưới đây?

15113.\dfrac{15}{113}.
17113.\dfrac{17}{113}.
13113.\dfrac{13}{113}.
11113.\dfrac{11}{113}.
Câu 9 (1đ):

Hàm số nào sau đây là hàm số chẵn?

y=tan⁡x2.y=\tan \dfrac{x}{2}.
y=sin⁡3x.y=\sin 3x.
y=sin⁡x.cos⁡x.y=\sin x.\cos x.
y=sin⁡2x.cos⁡x.y=\sin^2 x.\cos x.
Câu 10 (1đ):

Tập xác định của hàm số y=tan⁡x1−tan⁡xy=\dfrac{\tan x}{1-\tan x} là

D=R\{π2+kπ; π4+kπ ∣ k∈Z}D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi ; \, \dfrac{\pi }{4}+k\pi \, \big| \, k\in \mathbb{Z} \right\}.
D=R\{−π2+k2π; −π4+k2π ∣ k∈Z}D=\mathbb{R}\backslash \left\{ -\dfrac{\pi }{2}+k2\pi ; \, -\dfrac{\pi }{4}+k2\pi \, \big| \, k\in \mathbb{Z} \right\}.
D=R\{π2+kπ; π4+k2π ∣ k∈Z}D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi ; \, \dfrac{\pi }{4}+k2\pi \, \big| \, k\in \mathbb{Z} \right\}.
D=R\{π2+k2π; π4+k2π ∣ k∈Z}D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k2\pi ; \, \dfrac{\pi }{4}+k2\pi \, \big| \, k\in \mathbb{Z} \right\}.
Câu 11 (1đ):

Các nghiệm của phương trình sin⁡22x=1\sin^{2} 2x=1 là

x=π4+kπ2, (k∈Z)x=\dfrac{\pi }{4}+k\dfrac{\pi }{2}, \, (k \in \mathbb{Z}).
x=π2+kπ, (k∈Z)x=\dfrac{\pi }{2}+k\pi , \, (k \in \mathbb{Z}).
x=π8+kπ2, (k∈Z)x=\dfrac{\pi }{8}+k\dfrac{\pi }{2}, \, (k \in \mathbb{Z}).
x=kπ2, (k∈Z)x=k\dfrac{\pi }{2}, \, (k \in \mathbb{Z}).
Câu 12 (1đ):

Nghiệm của phương trình cos⁡x+sin⁡x=1\cos x+\sin x=1 là

x=k2π; x=π2+k2π, (k∈Z)x=k2\pi ;\,x=\dfrac{\pi }{2}+k2\pi, \, \left(k\in \mathbb{Z} \right).
x=π4+kπ; x=kπ, (k∈Z)x=\dfrac{\pi }{4}+k\pi ; \, x=k\pi, \, \left(k\in \mathbb{Z} \right).
x=kπ; x=−π2+k2π, (k∈Z)x=k\pi ; \, x=-\dfrac{\pi }{2}+k2\pi, \, \left(k\in \mathbb{Z} \right).
x=π6+kπ; x=k2π, (k∈Z)x=\dfrac{\pi }{6}+k\pi ; \, x=k2\pi, \, \left(k\in \mathbb{Z} \right).
Câu 13 (1đ):

Cho góc lượng giác xx, sao cho cos⁡x=−513\cos x=-\dfrac{5}{13} với 180∘<x<270∘180^\circ<x<270^\circ.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) sin⁡x<0\sin x<0.
b) tan⁡x=125\tan x=\dfrac{12}{5}.
c) cot⁡x=512\cot x=\dfrac{5}{12}.
d) sin⁡x−cos⁡x=−1213\sin x-\cos x=-\dfrac{12}{13}.
Câu 14 (1đ):

Cho hàm số f(x)=sin⁡2x+cos⁡x−1f(x)=\sin^2 x+\cos x-1.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Tập xác định của hàm số D=RD=\mathbb{R}.
b) f(−π)=−f(π)f(-\pi)=-f(\pi).
c) f(−x)=f(x)f(-x)=f(x).
d) Hàm số đã cho là hàm số chẵn.
Câu 15 (1đ):

Cho phương trình cos⁡2(π2−x)=sin⁡2(3x+π4)\cos^{2} \Big(\dfrac{\pi }{2}-x \Big)=\sin^{2}\Big(3x+\dfrac{\pi }{4} \Big) (*).

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hạ bậc hai vế của (*), ta được phương trình: 1+cos⁡(π−2x)2=1−cos⁡(6x+π2)2\dfrac{1+\cos \Big(\pi -2x \Big)}{2}=\dfrac{1-\cos \Big(6x+\dfrac{\pi }{2} \Big)}{2}.
b) Ta có: cos⁡(π−2x)=cos⁡2x\cos \Big(\pi -2x \Big)=\cos 2x.
c) Phương trình đã cho đưa về dạng: cos⁡2x=cos⁡6x\cos 2x=\cos 6x.
d) Nghiệm của phương trình đã cho là: x=kπ4, (k∈Z)x=k\dfrac{\pi }{4}, \, (k \in \mathbb{Z}).
Câu 16 (1đ):

Cho phương trình cos⁡2x=sin⁡(π4−x)\cos 2x=\sin \Big(\dfrac{\pi }{4}-x \Big) với x∈[0;π]x\in \Big[ 0;\pi \Big].

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Ta có: cos⁡2x=sin⁡(π2−2x)\cos 2x=\sin \Big(\dfrac{\pi }{2}-2x \Big).
b) Phương trình sin⁡(π2−2x)=sin⁡(π4−x)\sin \Big(\dfrac{\pi }{2}-2x \Big)=\sin \Big(\dfrac{\pi }{4}-x \Big) có các nghiệm là: x=π4+k2πx=\dfrac{\pi }{4}+k2\pi và x=5π4+k2π, (k∈Z)x=\dfrac{5\pi }{4}+k2\pi , \, (k \in \mathbb{Z})
c) Phương trình đã cho có bốn nghiệm thuộc đoạn [0;π]\Big[ 0;\pi \Big].
d) Tổng các nghiệm của phương trình đã cho trên đoạn [0;π]\Big[ 0;\pi \Big] là 5π6\dfrac{5\pi }{6}.
Câu 17 (1đ):

Cho cos⁡α=34\cos \alpha =\dfrac{3}{4}. Tính giá trị của biểu thức B=tan⁡α+3cot⁡αtan⁡α+cot⁡αB=\dfrac{\tan \alpha +3\cot \alpha }{\tan \alpha +\cot \alpha }. (làm tròn kết quả tới hàng phần trăm)

Trả lời:

Câu 18 (1đ):

Tìm giá trị mm nhỏ nhất để hàm số y=m−2sin⁡xy=\sqrt{m-2\sin x} xác định trên R\mathbb{R}.

Trả lời:

Câu 19 (1đ):

Tính tổng các nghiệm nguyên thuộc [−2 021 ; 2 021]\Big[ -2 \, 021\,;\,2 \, 021 \Big] của phương trình cos⁡[π3(2x−4x2+8x+20)]=1\cos \Big[ \dfrac{\pi }{3}\left(2x-\sqrt{4{{x}^{2}}+8x+20} \right) \Big]=1.

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP