

Phan Duy Khôi
Giới thiệu về bản thân
Chào mừng bạn đến với trang cá nhân của Phan Duy Khôi





0





0





0





0





0





0





0
2025-03-20 21:31:53
Để chứng minh phân số tối giản, ta chứng minh ƯCLN của tử số và mẫu số là 11.
Goi ƯCLN (n−1;n−2)=d⇒n−1:d(n−1;n−2)=d⇒n−1:d và n−2:dn−2:d
⇒(n−1)−(n−2):d⇒1:d⇒(n−1)−(n−2):d⇒1:d
⇒d=1⇒d=1 với mọi nn.
Vậy với mọi n∈Zn∈Z thì M=n−1n−2M=n−2n−1 là phân số tối giản.
2025-03-20 21:31:12
1. Trong hình vẽ có 4 bộ ba điểm thẳng là:
+) A,C,DA,C,D
+) A,B,EA,B,E
+) C,E,FC,E,F
+) D,E,BD,E,B
2.
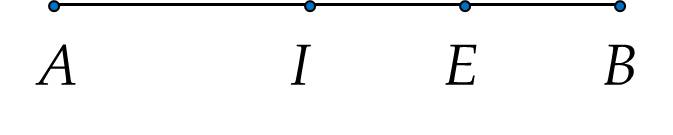
a) Theo hình vẽ, ta có: AI+IB=ABAI+IB=AB
Hay 4+IB=94+IB=9
IB=9−4=5IB=9−4=5 cm
b) Vì EE là trung điểm của IBIB nên
EI=EB=IB2=52=2,5EI=EB=2IB=25=2,5 (cm)
Theo hình vẽ, ta có: AE=AI+IE=4+2,5=6,5AE=AI+IE=4+2,5=6,5 (cm)