

thao_dung
Giới thiệu về bản thân



































+ \(S = \frac{1}{31} + \frac{1}{32} + \frac{1}{33} + \ldots + \frac{1}{60}\)
\(S < \left(\right. \frac{1}{30} + \frac{1}{30} + \ldots + \frac{1}{30} \left.\right) + \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right)\)
\(S < \frac{10}{30} + \frac{10}{40} + \frac{10}{50} < \frac{48}{60} = \frac{4}{5} ;\)
+ \(S > \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right) + \left(\right. \frac{1}{60} + \frac{1}{60} + \ldots + \frac{1}{60} \left.\right)\)
\(S > \frac{10}{40} + \frac{10}{50} + \frac{10}{60} > \frac{3}{5} .\)
1. a) \(O\) thuộc các đoạn thẳng: \(A B ; \&\text{nbsp}; C D ; \&\text{nbsp}; O A ; \&\text{nbsp}; O B ; \&\text{nbsp}; O C ; \&\text{nbsp}; O D .\)
b) Ta có \(O\) nằm giữa hai điểm \(A\) và \(B\) và \(O A \&\text{nbsp}; = \&\text{nbsp}; O B \&\text{nbsp}; = 3\) cm nên \(O\) là trung điểm của đoạn thẳng \(A B .\)
2. a) Số đo góc \(x O y\) bằng \(3 0^{\circ}\).
Hướng dẫn giải:
a) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)
\(= \frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)
\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. - \frac{25}{31} + \frac{- 6}{31} \left.\right)\)
\(= 1 + \left(\right. - 1 \left.\right)\)
\(= \&\text{nbsp}; 0\)
b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)
\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)
\(= \frac{17}{8} : \frac{49}{8}\)
\(= \frac{17}{49}\).
c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)
\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} \left.\right) + \frac{4}{5}\)
\(= \frac{1}{5} \cdot 1 + \frac{4}{5}\)
\(= \frac{1}{5} + \frac{4}{5} = 1.\)
d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)
\(= \frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)
\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)
\(= \frac{1}{30} - 2 + \frac{- 2}{3}\)
\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30}\)
\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30} = \frac{- 79}{30}\)
a) Ta có \(A D + D C = A C = A B = 15\) cm và \(\frac{A D}{D C} = \frac{A B}{B C} = \frac{15}{10} = \frac{3}{2}\).
Từ đó suy ra \(A D = 9\) cm, \(D C = 6\) cm.
b) Vì \(B D \bot B E\) nên \(B E\) là phân giác ngoài của góc \(B\) của tam giác \(A B C\).
Khi đó ta có \(\frac{A E}{E C} = \frac{A B}{B C}\).
Suy ra \(E C = \frac{A E . B C}{A B} = \frac{A E . 10}{15} = \frac{A E . 2}{3}\).
Suy ra \(3. C E = 2. \left(\right. A C + C E \left.\right)\) hay \(C E = 2. A C\).
Do đó \(C E = 30\) cm.
các số tự nhiên ngẫu nhiên có 2 hoặc 3 chữ số nhỏ hơn 200 là: {10;11;12...;199}
a) có 190 cáh viết số ngẫu nhiên
b) xác suất của biến cố "stn đc viết ra là số chia ht đc cho 2 và 5" là: 10; 20; 30; 40; 50; 60; 70; 80; 90; 100; 110; 120; 130; 140; 150; 160; 170; 180; 190\(\)
xs của biến cố là: \(\frac{18}{90}\)
xs của biến cố "stn đc viết ra là bình phương của 1 stn" là: 16; 25; 36; 49; 64; 81; 100; 121; 144; 169; 196
xs của biến cố là 11/90
a) Thị trường cung cấp nhiều nhất và ít nhất:
Nhiều nhất: Trung Quốc
Ít nhất: Lào
b)So sánh lượng cung cấp của Indonesia và Lào:
- Indonesia cung cấp 8.593 tấn.
- Lào cung cấp 447 tấn.
- Mức tăng của Indonesia so với Lào là: (8.593 : 447) x 100% xấp xỉ 1922,4%
- Vậy lượng tinh bột sắn mà Indonexia cung cấp cho Đài Loan trong 9 tháng năm 2022 tăng khoảng 1922,4% so với thị trường Lào.
c)
- Tổng số lượng tinh bột sắn mà các nước đã cung cấp là: 218 + 1552 + 8593 + 447 + 483 = 11293 (tấn)
- Tỉ lệ phần trăm tinh bột sắn mà Lào cung cấp là: (447:11293) x 100% = 3.95%
- Vậy nhận định thị trường lào cung cấp tinh bột sắn chiếm khoảng 1,2% là không chính xác.
a) Hoa thu được dữ liệu trên bằng cách làm thí nghiệm (đo nhiệt độ nước tại một số thời điểm khi bắt đầu đun).
b) Giá trị 105105 là giá trị không hợp lí vì ở điều kiện bình thường, nước sôi ở 100100 độ C và sẽ bay hơi.
2)
a)
| Điểm | 55 | 66 | 77 | 88 |
| Số bạn | 22 | 33 | 33 | 22 |
b) Đối tượng thống kê: Điểm kiểm tra môn Ngữ văn.
Tiêu chí thống kê: Điểm kiểm tra môn Ngữ văn được thống kê theo từng bạn trong tổ 1.
1)
a) Có 33 kết quả khác nhau trong mỗi lần lấy bóng là:
- Hòa lấy ra quả bóng đỏ (kí hiệu: Đ).
- Hòa lấy ra quả bóng xanh (kí hiệu: X).
- Hòa lấy ra quả bóng vàng (kí hiệu: V).
b) Hai điều chú ý của mô hình xác suất là:
- Hòa lấy ra ngẫu nhiên một quả bóng trong hộp.
- Tập hợp các kết quả có thể xảy ra là: {Đ, X, V}. Các kí hiệu được giải thích ở phần trên.
c) Trong 99 lần lấy ngẫu nhiên, có 44 lần bạn Hòa lấy ra quả bóng màu Xanh.
Xác suất thực nghiệm của kết quả bạn Hòa lấy ra quả bóng màu Xanh là:
4:9=494:9=
4/9
a) Tập hợp các điểm thuộc đoạn thẳng BDBD là B;C;DB;C;D, tập hợp các điểm thuộc không đoạn thẳng BDBD là A;EA;E.
b) Cặp đường thẳng song song là ABAB // DEDE.
c) Gợi ý: Liệt kê theo các giao điểm, có 5 giao điểm nên có 5 cặp đường thẳng cắt nhau.
Các cặp đường thẳng cắt nhau là
ABAB và AEAE cắt nhau tại AA.
BABA và BDBD cắt nhau tại BB.
AEAE và BDBD cắt nhau tại CC.
DEDE và DBDB cắt nhau tại DD.
EAEA và EDED cắt nhau tại EE.
2)
a)
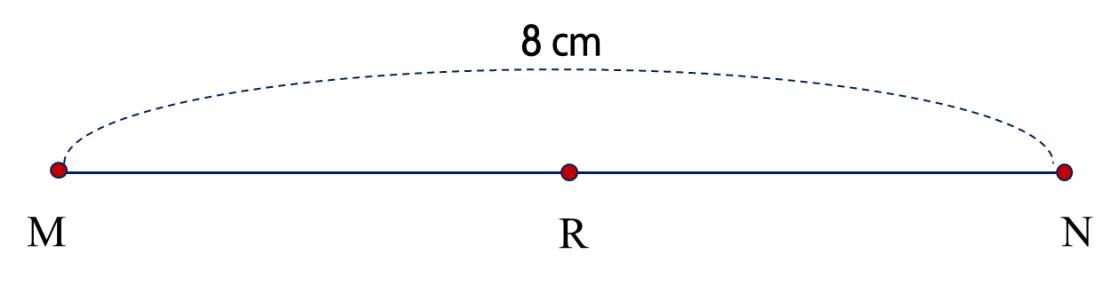
Vì RR là trung điểm của đoạn thẳng MNMN, nên ta có MR=RN=MN:2MR=RN=MN:2.
Độ dài của đoạn thẳng MRMR hay RNRN là:
8:2=48:2=4 (cm)
b)
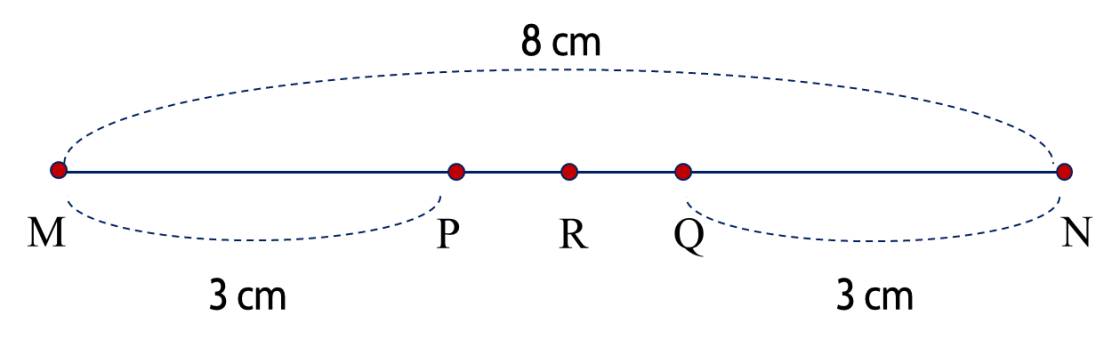
Nhìn hình vẽ, ta thấy RR nằm giữa PP và QQ; MN=MP+PQ+QNMN=MP+PQ+QN; MR=MP+PRMR=MP+PR.
Độ dài của đoạn thẳng PQPQ là
8−3−3=28−3−3=2 (cm).
Độ dài của đoạn thẳng PRPR là
4−3=14−3=1 (cm).
Từ đây, ta thấy PR:PQ=12PR:PQ=21,
Vậy RR là trung điểm PQPQ.
3)
Chọn 1 điểm nối với 1111 điểm còn lại ta được 1111 đường thẳng, làm như thế với 1212 điểm ta được 12.(12−1)=13212.(12−1)=132 đường thẳng. Nhưng mỗi đường thẳng lặp lại 22 lần nên số đường thẳng vẽ được là 132:2=66132:2=66 đường thẳng.
Qua 44 điểm không thẳng hàng sẽ vẽ được 66 đường thẳng.
Qua 44 điểm thẳng hàng vẽ được 11 đường thẳng nên số đường thẳng giảm đi 55 đường thẳng
Vậy số đường thẳng vẽ được là 66−5=6166−5=61 đường thẳng vậy ta vẽ được 61 đường thẳng.
a) Có 33 kết quả khác nhau trong mỗi lần lấy bóng là:
- Hòa lấy ra quả bóng đỏ (kí hiệu: Đ).
- Hòa lấy ra quả bóng xanh (kí hiệu: X).
- Hòa lấy ra quả bóng vàng (kí hiệu: V).
b) Hai điều chú ý của mô hình xác suất là:
- Hòa lấy ra ngẫu nhiên một quả bóng trong hộp.
- Tập hợp các kết quả có thể xảy ra là: {Đ, X, V}. Các kí hiệu được giải thích ở phần trên.
c) Trong 99 lần lấy ngẫu nhiên, có 44 lần bạn Hòa lấy ra quả bóng màu Xanh.
Xác suất thực nghiệm của kết quả bạn Hòa lấy ra quả bóng màu Xanh là:
4:9=494:9=\(\dfrac{ }{ }\)4/9