D(x)=2(x2−x)+(3y2−2y)+(4z2−2z)+2

\(= 2 \left(\right. x^{2} - x + \frac{1}{4} \left.\right) + 3 \left(\right. y^{2} - \frac{2}{3} y + \frac{1}{9} \left.\right) + \left[\right. \left(\right. 2 z \left.\right)^{2} - 2 z + \frac{1}{4} \left]\right. + 2 - \frac{1}{2} - \frac{1}{3} - \frac{1}{4}\)

\(= 2 \left(\left(\right. x - \frac{1}{2} \left.\right)\right)^{2} + 3 \left(\left(\right. y - \frac{1}{3} \left.\right)\right)^{2} + \left(\left(\right. 2 z - \frac{1}{2} \left.\right)\right)^{2} + \frac{11}{2} \geq \frac{11}{2}\)

Vậy giá trị nhỏ nhất của \(D\) là: \(\frac{11}{2}\) tại \(\left(\right. x , y , z \left.\right) = \left(\right. \frac{1}{2} ; \frac{1}{3} ; \frac{1}{4} \left.\right)\).

a) Qua \(D\) vẽ một đường thẳng song song với \(B M\) cắt \(A C\) tại \(N\).

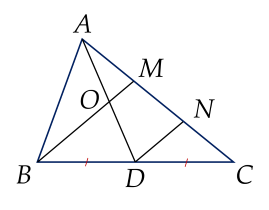
Xét \(\Delta M B C\) có \(D B = D C\) và \(D N\) // \(B M\) nên \(M N = N C = \frac{1}{2} M C\) (định lí đường trung bình của tam giác).

Mặt khác \(A M = \frac{1}{2} M C\), do đó \(A M = M N = \frac{1}{2} M C\).

Xét \(\Delta A N D\) có \(A M = M N\) và \(B M\) // \(D N\) nên \(O A = O D\) hay \(O\) là trung điểm của \(A D\).

b) Xét \(\Delta A N D\) có \(O M\) là đường trung bình nên \(O M = \frac{1}{2} D N\) (1) 

Xét \(\Delta M B C\) có \(D N\) là đường trung bình nên \(D N = \frac{1}{2} B M\). (2)

Từ (1) và (2) ta có \(O M = \frac{1}{4} B M\).

a) Tổng số học sinh của lớp là: 40.

Số học sinh Tốt chiếm số phần trăm là:

     16 : 40 . 100% = 40%

Số học sinh Khá chiếm số phần trăm là:

     11 : 40 . 100% = 27,5%

b) Số học sinh xếp loại Chưa đạt chiếm số phần trăm là:

     3 : 40 . 100% = 7,5%

Cô giáo thông báo tỉ lệ học sinh xếp loại Chưa đạt của lớp chiếm trên 7% là đúng.