Phần tự luận (7 điểm)

Bài 1

Thực hiện phép tính (tính bằng cách hợp lí nếu có thể):

a) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\);

b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\);

c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\);

d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\).

Hướng dẫn giải:

a) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. - \frac{25}{31} + \frac{- 6}{31} \left.\right)\)

\(= 1 + \left(\right. - 1 \left.\right)\)

\(= \&\text{nbsp}; 0\)

b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)

\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)

\(= \frac{17}{8} : \frac{49}{8}\)

\(= \frac{17}{49}\).

c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)

\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} \left.\right) + \frac{4}{5}\)

\(= \frac{1}{5} \cdot 1 + \frac{4}{5}\)

\(= \frac{1}{5} + \frac{4}{5} = 1.\)

d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30} = \frac{- 79}{30}\)

) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. - \frac{25}{31} + \frac{- 6}{31} \left.\right)\)

\(= 1 + \left(\right. - 1 \left.\right)\)

\(= \& \text{nbsp} ; 0\)

b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)

\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)

\(= \frac{17}{8} : \frac{49}{8}\)

\(= \frac{17}{49}\).

c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)

\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} \left.\right) + \frac{4}{5}\)

\(= \frac{1}{5} \cdot 1 + \frac{4}{5}\)

\(= \frac{1}{5} + \frac{4}{5} = 1.\)

d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30} = \frac{- 79}{30}\)

Bài 2

1. Quan sát hình vẽ:

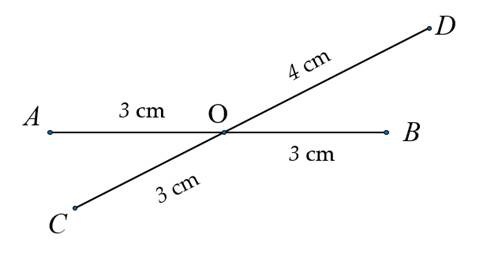
a) Điểm \(O\) thuộc những đoạn thẳng nào?

b) Điểm \(O\) là trung điểm của đoạn thẳng nào?

2. a) Dùng thước đo góc xác định số đo góc \(x O y\).

b) Vẽ góc \(m A n\) có số đo bằng \(15 0^{\circ}\).

Hướng dẫn giải:

1. a) \(O\) thuộc các đoạn thẳng: \(A B ; \&\text{nbsp}; C D ; \&\text{nbsp}; O A ; \&\text{nbsp}; O B ; \&\text{nbsp}; O C ; \&\text{nbsp}; O D .\)

b) Ta có \(O\) nằm giữa hai điểm \(A\) và \(B\) và \(O A \&\text{nbsp}; = \&\text{nbsp}; O B \&\text{nbsp}; = 3\) cm nên \(O\) là trung điểm của đoạn thẳng \(A B .\)

2. a) Số đo góc \(x O y\) bằng \(3 0^{\circ}\).

b)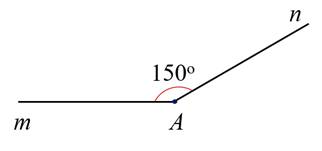 

a) \(O\) thuộc các đoạn thẳng: \(A B ; \& \text{nbsp} ; C D ; \& \text{nbsp} ; O A ; \& \text{nbsp} ; O B ; \& \text{nbsp} ; O C ; \& \text{nbsp} ; O D .\)

b) Ta có \(O\) nằm giữa hai điểm \(A\) và \(B\) và \(O A \& \text{nbsp} ; = \& \text{nbsp} ; O B \& \text{nbsp} ; = 3\) cm nên \(O\) là trung điểm của đoạn thẳng \(A B .\)

2. a) Số đo góc \(x O y\) bằng \(3 0^{\circ}\).

b) 

Bài 3

Một cửa hàng bán bóng rổ thống kê lại số lượng bóng bán được trong ba tháng đầu năm 2024 trong hình bên dưới.

a) Tính số lượng bóng rổ bán được trong tháng 1, tháng 2 và tháng 3.

b) Trong ba tháng, cửa hàng bán được tổng cộng bao nhiêu quả bóng rổ?

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3 bao nhiêu quả bóng rổ?

d) Tính tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2.

Hướng dẫn giải:

a) Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:

\(15\) quả; \(20\) quả; \(10\) quả.

b) Cả ba tháng cửa hàng bán được:

\(15 + 20 + 10 = 45\) (quả)

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:

\(20 – 10 = 10\) (quả)

d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:

\(3 : 4 = \frac{3}{4}\)

Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:

\(15\) quả; \(20\) quả; \(10\) quả.

b) Cả ba tháng cửa hàng bán được:

\(15 + 20 + 10 = 45\) (quả)

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:

\(20 – 10 = 10\) (quả)

d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:

\(3 : 4 = \frac{3}{4}\)

Bài 4

Cho \(S = \frac{1}{31} + \frac{1}{32} + \frac{1}{33} + \ldots + \frac{1}{60}\).

Chứng minh rằng: \(\frac{3}{5} < S < \frac{4}{5}\)

+ \(S = \frac{1}{31} + \frac{1}{32} + \frac{1}{33} + \ldots + \frac{1}{60}\)

\(S < \left(\right. \frac{1}{30} + \frac{1}{30} + \ldots + \frac{1}{30} \left.\right) + \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right)\)

\(S < \frac{10}{30} + \frac{10}{40} + \frac{10}{50} < \frac{48}{60} = \frac{4}{5} ;\)

+ \(S > \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right) + \left(\right. \frac{1}{60} + \frac{1}{60} + \ldots + \frac{1}{60} \left.\right)\)

\(S > \frac{10}{40} + \frac{10}{50} + \frac{10}{60} > \frac{3}{5} .\)

Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:

\(15\) quả; \(20\) quả; \(10\) quả.

b) Cả ba tháng cửa hàng bán được:

\(15 + 20 + 10 = 45\) (quả)

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:

\(20 – 10 = 10\) (quả)

d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:

\(3 : 4 = \frac{3}{4}\)

a) \(O\) thuộc các đoạn thẳng: \(A B ; \&\text{nbsp}; C D ; \&\text{nbsp}; O A ; \&\text{nbsp}; O B ; \&\text{nbsp}; O C ; \&\text{nbsp}; O D .\)

b) Ta có \(O\) nằm giữa hai điểm \(A\) và \(B\) và \(O A \&\text{nbsp}; = \&\text{nbsp}; O B \&\text{nbsp}; = 3\) cm nên \(O\) là trung điểm của đoạn thẳng \(A B .\)

2. a) Số đo góc \(x O y\) bằng \(3 0^{\circ}\).

b) 

) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. - \frac{25}{31} + \frac{- 6}{31} \left.\right)\)

\(= 1 + \left(\right. - 1 \left.\right)\)

\(= \&\text{nbsp}; 0\)

b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)

\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)

\(= \frac{17}{8} : \frac{49}{8}\)

\(= \frac{17}{49}\).

c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)

\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} \left.\right) + \frac{4}{5}\)

\(= \frac{1}{5} \cdot 1 + \frac{4}{5}\)

\(= \frac{1}{5} + \frac{4}{5} = 1.\)

d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30} = \frac{- 79}{30}\)