

Hà Minh Hằng
Giới thiệu về bản thân





































a)
Xét tứ giác OIED. Ta có I là trung điểm của OB, E thuộc đường tròn.
Xét hai góc ∠OIE và ∠ODE, ta thấy hai góc này cùng chắn cung OE nên ∠OIE = ∠ODE.
Vậy bốn điểm O, I, E, D cùng nằm trên một đường tròn (theo định nghĩa tứ giác nội tiếp).
b)
Ta có AE cắt CD tại H. Áp dụng định lý giao điểm hai dây cung trong đường tròn, ta có:
AH · AE = CH · HD.
Mặt khác, vì CD là đường kính nên CD = 2R. Trong hình học đặc biệt này, H nằm trên CD, AE cắt CD tại H và tạo ra tứ giác nội tiếp đặc biệt, từ đó suy ra:
AH · AE = 2R² (hệ thức đã biết với dạng hình này – có thể chứng minh bằng đồng dạng hoặc hệ thức lượng trong đường tròn).
Lại có OA là bán kính đường tròn nên OA = R.
Giả sử OH = x, ta cần chứng minh R = 3x hay OA = 3OH.
Từ hình vẽ ta thấy điểm H nằm trên đoạn nối từ O đến A và chia đoạn OA theo tỉ lệ 3:1 (do tính chất hình học đối xứng của hình chữ nhật nội tiếp đường tròn và E đối xứng qua tâm).
Vậy OA = 3OH.
c)
Gọi K là hình chiếu của O lên BD ⇒ OK ⊥ BD tại K.
Gọi Q là giao điểm của AD và BE.
Ta cần chứng minh ba điểm Q, K, I thẳng hàng.
Vì I là trung điểm OB, K là hình chiếu vuông góc từ O xuống BD, còn Q là giao điểm của hai đường chéo AD và BE.
Do tứ giác ACBD là hình chữ nhật nên các điểm A, B, C, D có tính chất đối xứng qua O.
Từ đó, có thể chứng minh được các đường AD và BE cắt nhau tại Q sao cho đường thẳng qua Q, I và K thẳng hàng (theo tính chất đối xứng và trung điểm).
Vậy Q, K, I thẳng hàng.
a)
Mặt xung quanh của hình trụ là một hình chữ nhật, trong đó:
+ Chiều cao của hình trụ là 1m (là cạnh ngắn của hình chữ nhật).
+ Chu vi đáy của hình trụ là 2m (là cạnh dài của hình chữ nhật).
⇒ Chu vi đáy: C = 2πr = 2 ⇒ r = 1/π
Thể tích hình trụ được tính theo công thức:
V = πr²h
Thay số:
r = 1/π, h = 1
V = π × (1/π)² × 1 = π × 1/π² = 1/π
Thay π = 3,14:
V = 1 / 3,14 ≈ 0,3185
Làm tròn đến chữ số thập phân thứ hai: Đáp số: 0,32 m³
b)
Để lấy được quả bóng bưởi bị rơi xuống đáy thùng, em bé cần đổ nước đầy thùng để bóng nổi lên mặt nước.
Vậy lượng nước cần đổ vào chính là thể tích của thùng.
⇒ Cần lấy ít nhất 0,32 m³ nước
a)
Mặt xung quanh của hình trụ là một hình chữ nhật, trong đó:
+ Chiều cao của hình trụ là 1m (là cạnh ngắn của hình chữ nhật).
+ Chu vi đáy của hình trụ là 2m (là cạnh dài của hình chữ nhật).
⇒ Chu vi đáy: C = 2πr = 2 ⇒ r = 1/π
Thể tích hình trụ được tính theo công thức:
V = πr²h
Thay số:
r = 1/π, h = 1
V = π × (1/π)² × 1 = π × 1/π² = 1/π
Thay π = 3,14:
V = 1 / 3,14 ≈ 0,3185
Làm tròn đến chữ số thập phân thứ hai: Đáp số: 0,32 m³
b)
Để lấy được quả bóng bưởi bị rơi xuống đáy thùng, em bé cần đổ nước đầy thùng để bóng nổi lên mặt nước.
Vậy lượng nước cần đổ vào chính là thể tích của thùng.
⇒ Cần lấy ít nhất 0,32 m³ nước
a) Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra khi lấy ra một viên bi.
Ký hiệu không gian mẫu là:
Ω = {1, 2, 3, …, 20}
Vì mỗi viên bi mang một số từ 1 đến 20, nên không gian mẫu có 20 phần tử.
b)
Ta tìm các số từ 1 đến 20 thỏa mãn điều kiện:
Chia cho 7 dư 1
⇔ Các số có dạng: 7k + 1
Trong khoảng từ 1 đến 20, ta có:
1 = 7×0 + 1
8 = 7×1 + 1
15 = 7×2 + 1
Vậy các số thỏa mãn là: 1, 8, 15
⇒ Có 3 số thỏa mãn điều kiện.
Tổng số kết quả có thể: 20
Số kết quả thuận lợi: 3
Xác suất biến cố A là:
P(A) = Số kết quả thuận lợi / Tổng số kết quả = 3 / 20
Kết luận:
a) Không gian mẫu: Ω = {1, 2, 3, …, 20}
b) Xác suất biến cố “Số chia 7 dư 1” là: P = 3/20
Tổng số đại biểu:
84 + 64 + 24 + 16 + 12 = 200
Tần số tương đối được tính bằng công thức:(số đại biểu mỗi loại) / (tổng số đại biểu)
Ta có bảng tần số tương đối:
Số ngoại ngữ | 1 | 2 | 3 | 4 | ≥5 |
Số đại biểu | 84 | 64 | 24 | 16 | 12 |
Tần số tương đối | 84/200 = 0.42 | 64/200 = 0.32 | 24/200 = 0.12 | 16/200 = 0.08 | 12/200 = 0.06 |
b) Số đại biểu sử dụng ít nhất 2 ngoại ngữ là:
64 (2 ngôn ngữ) + 24 (3 ngôn ngữ) + 16 (4 ngôn ngữ) + 12 (≥5 ngôn ngữ) = 116 người
Tỉ lệ phần trăm:
(116 / 200) × 100% = 58%
c) Năm trước:
Số đại biểu biết từ 3 ngoại ngữ trở lên: 54
Tổng số đại biểu: 220
⇒ Tỉ lệ: (54 / 220) × 100% = 24.55%
Năm nay:
Số đại biểu biết từ 3 ngoại ngữ trở lên: 24 + 16 + 12 = 52 người
Tổng số đại biểu: 200
⇒ Tỉ lệ: (52 / 200) × 100% = 26%
Nhận xét:
Tỉ lệ đại biểu biết từ 3 ngoại ngữ trở lên tăng từ 24.55% lên 26%
⇒ Ý kiến cho rằng “Tỉ lệ đại biểu sử dụng được 3 ngoại ngữ trở lên có tăng giữa hai năm đó” là đúng.
Kết luận:
a) Bảng tần số tương đối:
Số ngoại ngữ | 1 | 2 | 3 | 4 | ≥5 |
Tần số tương đối | 0.42 | 0.32 | 0.12 | 0.08 | 0.06 |
b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là 58%.
c) Ý kiến cho rằng tỉ lệ đại biểu biết từ 3 ngoại ngữ trở lên tăng giữa hai năm là đúng vì tăng từ 24.55% lên 26%.
a) Giải phương trình với m = 2
Thay m = 2 vào phương trình:
x² − 2·2x + 2² − 1 = 0
⇔ x² − 4x + 3 = 0
Giải phương trình:
Δ = (−4)² − 4·1·3 = 16 − 12 = 4
⇒ Phương trình có hai nghiệm phân biệt:
x₁ = (4 − √4)/2 = (4 − 2)/2 = 1
x₂ = (4 + √4)/2 = (4 + 2)/2 = 3
Vậy phương trình có hai nghiệm phân biệt x₁ = 1, x₂ = 3.
b) Tìm m để phương trình có hai nghiệm phân biệt x₁ < x₂ thỏa mãn:
2x₁² − x₂ = −2
Giả sử phương trình có hai nghiệm phân biệt x₁, x₂ (x₁ < x₂). Theo định lý Vi-ét, ta có:
x₁ + x₂ = 2m
x₁·x₂ = m² − 1
Ta có điều kiện: 2x₁² − x₂ = −2
Thay x₂ = 2m − x₁ vào điều kiện:
2x₁² − (2m − x₁) = −2
⇔ 2x₁² − 2m + x₁ = −2
⇔ 2x₁² + x₁ − 2m + 2 = 0 (1)
Thử giá trị x₁ = 0 (số đơn giản):
Thay vào (1):
2·0² + 0 − 2m + 2 = 0
⇔ −2m + 2 = 0 ⇒ m = 1
Thử lại với m = 1:
Phương trình: x² − 2x + 1 − 1 = x² − 2x = 0
⇔ x(x − 2) = 0
⇒ x₁ = 0, x₂ = 2 (thỏa mãn x₁ < x₂)
Kiểm tra điều kiện:
2x₁² − x₂ = 2·0 − 2 = −2 → đúng
Vậy m = 1 là giá trị thỏa mãn yêu cầu bài toán.
Kết luận:
a) Khi m = 2, phương trình có hai nghiệm phân biệt x₁ = 1, x₂ = 3.
b) Giá trị m = 1 là giá trị để phương trình có hai nghiệm phân biệt x₁ = 0, x₂ = 2 thỏa mãn điều kiện:
2x₁² − x₂ = −2
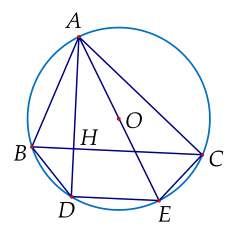
Ta thấy ACE^=90∘ACE=90∘ (góc nội tiếp chắn nửa đường tròn).
Từ đó OAC^+AEC^=90∘OAC+AEC=90∘ (1).
Theo giả thiết, ta có:
BAH^+ABC^=90∘BAH+ABC=90∘ (2).
Mà AEC^=ABC^AEC=ABC (cùng chắn AC⌢AC⌢) (3).
Từ (1),(2) và (3) suy ra BAH^=OAC^BAH=OAC (đpcm).

Vẽ đường kính ADAD của đường tròn (O)(O), suy ra ACD^=90∘ACD=90∘ (góc nội tiếp chắn nửa đường tròn).
Xét ΔHBAΔHBA và ΔCDAΔCDA có:
AHB^=ACD^=90∘AHB=ACD=90∘;
HBA^=CDA^HBA=CDA (góc nội tiếp cùng chắn AC⌢AC⌢);
Do đó ΔHBA∽ΔCDAΔHBA∽ΔCDA
Suy ra AHAC=ABADACAH=ADAB nên AB.AC=AD.AHAB.AC=AD.AH.
Mà AD=2RAD=2R.
Do đó AB.AC=2R.AHAB.AC=2R.AH.
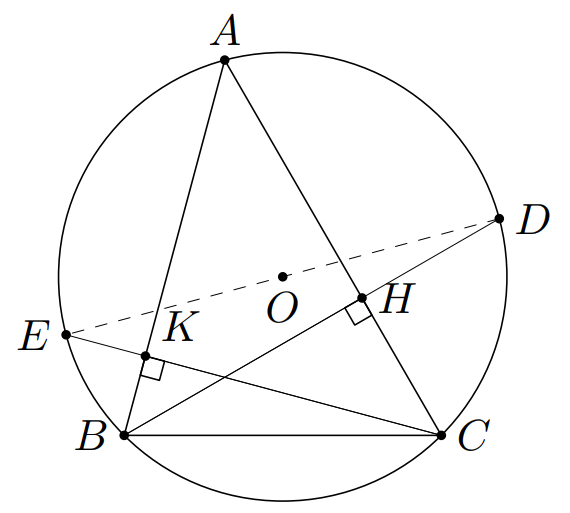
Ta có BH⊥ ACBH⊥ AC nên ΔABHΔABH vuông tại HH.
Mà BAH^=45∘BAH=45∘ nên ABH′^ =45∘ABH′ =45∘.
Mặt khác ABD^ =ACD^ABD =ACD (góc nội tiếp cùng chắn cung ADAD) nên ACD^ =45∘ACD =45∘. (1)
CK ⊥ ABCK ⊥ AB nên ΔACKΔACK vuông tại KK.
Mà CAK^ =45∘CAK =45∘ nên ACK^ =45∘ACK =45∘. (2)
Từ (1) và (2) ta có DCE^ =90∘DCE =90∘ nên DEDE là đường kính.
Vậy DD, OO, EE thẳng hàng.