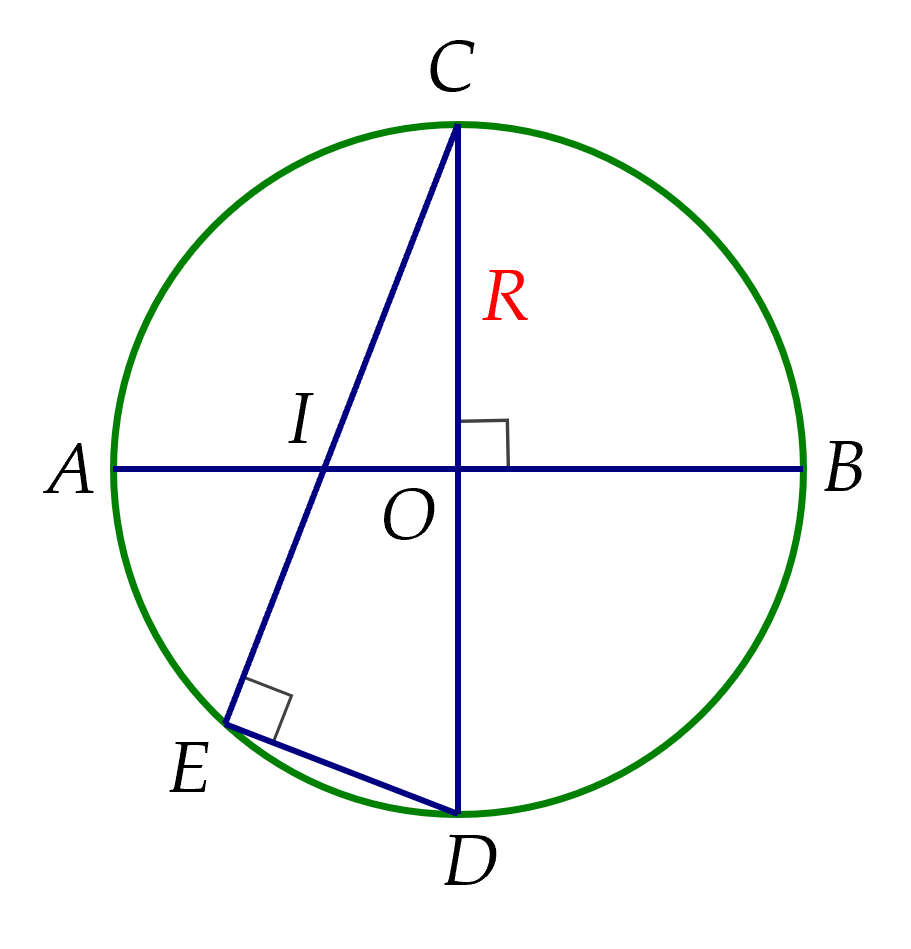
Ta có AI=2AO3=2R3AI=32AO​=32R​ suy ra OI=R−2R3=R3OI=R−32R​=3R​

$\Delta OCI$ vuông tại $O$, ta có:

CI=OC2+OI2=R2+(R3)2=R103CI=OC2+OI2​=R2+(3R​)2​=3R10​​ nội tiếp đường tròn  có cạnh $CD$ là đường kính

Suy ra $\Delta CED$ vuông tại $E$

Hai tam giác vuông $OCI$ và $CED$ có C^C :chung 

Suy ra $\Delta COI\backsim \Delta CED$

Suy ra COCE=CICDCECO​=CDCI​

CE=CO.CDCI=R.2RR103=6R10=3R105CE=CICO.CD​=R310​​R.2R​=10​6R​=53R10​​.

a) Gọi $E,F$ là tiếp điểm của đường tròn $(I)$ với các cạnh $AB,AC$

Theo tính chất của hai tiếp tuyến cắt nhau, ta có: $AE=AF;BE=BD;CD=CF$

Do đó: $2BD=BD+BE=BC-CD+AB-AE$

$=BC+AB-(CD+AE)=BC+AB-(CF+AF)$

$=BC+AB-AC$ suy ra BD=BC+AB−AC2BD=2BC+AB−AC​

b) Tương tự câu a) ta có: DC=BC+AC−AB2DC=2BC+AC−AB​ mà AB2+AC2=BC2AB2+AC2=BC2 ($\Delta ABC$ vuông tại $A$), do đó:

BD.DC=(BC+AB−AC)(BC+AC−AB)4BD.DC=4(BC+AB−AC)(BC+AC−AB)​

BC2−(AB−AC)24=BC2−AB2−AC2+2AB.AC44BC2−(AB−AC)2​=4BC2−AB2−AC2+2AB.AC​

=AB.AC2=SABC=2AB.AC​=SABC​.

IG=1cm

r=2cm