Việc nhà văn mượn lời người bán phở bò đánh giá về phở gà như trên có tác dụng giúp cho câu văn thêm phần phong phú và thuyết phục.

Ta có: \(\frac{x - a}{b c} + \frac{x - b}{c a} + \frac{x - c}{a b} = \frac{2}{a} + \frac{2}{b} + \frac{2}{c}\)

\(\left(\right. \frac{x - a}{b c} - \frac{2}{a} \left.\right) + \left(\right. \frac{x - b}{c a} - \frac{2}{b} \left.\right) + \left(\right. \frac{x - c}{a b} - \frac{2}{c} \left.\right) = 0\)

\(\frac{a \left(\right. x - a \left.\right) - 2 b c + b \left(\right. x - b \left.\right) - 2 c a + c \left(\right. x - c \left.\right) - 2 a b}{a b c} = 0\)

Điều kiện xác định: \(a , b , c \neq 0\)

Khi đó: \(\frac{\left(\right. a + b + c \left.\right) x - a^{2} - 2 b c - b^{2} - 2 c a - c^{2} - 2 a b}{a b c} = 0\)

\(\left(\right. a + b + c \left.\right) x = \left(\left(\right. a + b + c \left.\right)\right)^{2}\) 

+ Nếu \(a + b + c = 0\) thì phương trình có vô số nghiệm.

+ Nếu \(a + b + c \neq 0\) thì phương trình có nghiệm duy nhất \(x = a + b + c\).

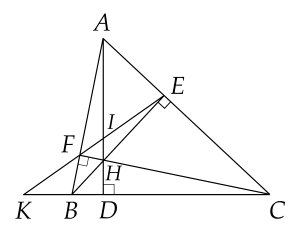
a) Xét \(\Delta A B E\) và \(\Delta A C F\) có:

\(\hat{B A C}\) chung;

\(\hat{A E B} = \hat{A F C} = 90^{\circ}\);

Do đó \(\Delta A B E \sim \Delta A C F\) (g.g).

Suy ra \(\frac{A B}{A C} = \frac{A E}{A F}\) nên \(A B . A F = A C . A E\).

b) Từ \(A B . A F = A C . A E\) suy ra \(\frac{A E}{A F} = \frac{A B}{A C}\).

Xét \(\Delta A E F\) và \(\Delta A B C\) có:

\(\frac{A E}{A F} = \frac{A B}{A C}\) (cmt);

\(\hat{B A C}\) chung;

Do đó \(\Delta A E F \sim \Delta A B C\) (c.g.c)

Suy ra \(\hat{A F E} = \hat{A C B}\) (cặp góc tương ứng).

c) Xét \(\Delta C E B\) và \(\Delta C D A\) có:

\(\hat{A C B}\) chung;

\(\hat{C E B} = \hat{C D A} = 90^{\circ}\)

Do đó \(\Delta C E B \sim \Delta C D A\) (g.g)

Suy ra \(\frac{C B}{C E} = \frac{C A}{C D}\) (cặp cạnh tương ứng).

Xét \(\Delta C B A\) và \(\Delta C E D\) có:

\(\frac{C B}{C E} = \frac{C A}{C D}\) (cmt);

\(\hat{A C B}\) chung;

Do đó \(\Delta C B A \sim \Delta C E D\) (c.g.c)

Suy ra \(\hat{C D E} = \hat{C A B}\) (cặp góc tương ứng) (1)

Tương tự: \(\hat{B D F} = \hat{C A B}\) (2).

Từ (1) và (2) suy ra \(\hat{C D E} = \hat{B D F}\).

Mà \(\hat{C D E} + \hat{E D A} = \hat{B D F} + \hat{F D A}\) suy ra \(\hat{E D A} = \hat{F D A}\).

Suy ra \(D A\) là phân giác của góc \(E D F\).

Mặt khác \(A D \bot K D\) nên \(D K\) là phân giác ngoài của \(\Delta D E F\).

Ta có \(D I\) là phân giác trong của \(\Delta \&\text{nbsp}; D E F\) suy ra \(\frac{I F}{I E} = \frac{D F}{D E}\) (3)

Ta có \(D K\) là phân giác ngoài của \(\Delta D E F\) suy ra \(\frac{K F}{K E} = \frac{D F}{D E}\) (4)

Từ (3) và (4) suy ra \(\frac{I F}{I E} = \frac{K F}{K E}\).

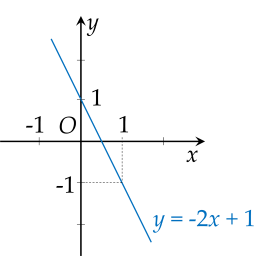
a) Với \(m = - 1\), hàm số trở thành \(y = - 2 x + 1\).

Xét hàm số \(y = - 2 x + 1\) :

Thay \(x = 0\) thì \(y = 1\).

Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 0 ; 1 \left.\right)\).

Thay \(x = 1\) thì \(y = - 1\).

Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 1 ; - 1 \left.\right)\).

Vẽ đồ thị:

b) Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) song song với đường thẳng \(\left(\right. d^{'} \&\text{nbsp}; \left.\right) : y = - 3 x + 9\) nên: \(a \neq - 3 ; b \neq 9\).

Khi đó ta có: \(\left(\right. d \left.\right) : y = - 3 x + b\) và \(b \neq 9\).

Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) đi qua \(A \left(\right. 1 ; - 8 \left.\right)\) nên: \(- 8 = - 3.1 + b\)

Suy ra \(b = - 5\) (thoả mãn)

Vậy đường thẳng cần tìm là \(\left(\right. d \left.\right) : y = - 3 x - 5\).

a

a) \(3 x - 5 = 4\)

\(3 x = 9\)

\(x = 3\)

Vậy phương trình có nghiệm \(x = 3\).

b) \(\frac{2 x}{3} + \frac{3 x - 1}{6} = \frac{x}{2}\)

\(\frac{4 x}{6} + \frac{3 x - 1}{6} = \frac{3 x}{6}\)

\(4 x + 3 x - 1 = 3 x\)

\(4 x = 1\)

\(x = \frac{1}{4}\)

bjgjfytryutyhu

- Không đầu hàng trước những khó khăn trong cuộc sống.

- Trong bất cứ hoàn cảnh nào, sự hi vọng, nỗ lực, dũng cảm sẽ đem đến cho chúng ta sức mạnh .

- Trong cuộc sống, sự hi vong và nỡ lực giúp chúng ta có tinh thần lạc quan, xóa đi mệt mỏi, giúp chúng ta giải quyết vấn đề, là động lực giúp chúng ta vượt qua khó khăn, thử thách. 

-Người nông dân : Lúc đầu định giúp con lừa nhưng nghĩ rằng lừa đã già và cái giếng cũng cần lấp lại nên nhanh chóng buông xuôi, bỏ cuộc.

-Con lừa : lúc đầu kêu la thảm thiết, muốn thoát ra khỏi giếng nhưng rồi khôn ngoan, dùng chính những xẻng đất muốn vùi lấp nó để tự giúp nó thoát khỏi giếng.