Coi hệ gồm hai viên bi là một hệ kín.

Theo định luật bảo toàn động lượng ta có:

\(\overset{\rightarrow}{p_{1}} + \overset{\rightarrow}{p_{2}} = \overset{\rightarrow}{p}\) hay  \(m_{1} \left(\overset{\rightarrow}{\text{v}}\right)_{1} + m_{2} \left(\overset{\rightarrow}{\text{v}}\right)_{2} = \left(\right. m_{1} + m_{2} \left.\right) \overset{\rightarrow}{\text{v}}\)

a. Sau va chạm chúng dính vào nhau và chuyển động với vận tốc \(\text{v}\) = 3m/s theo hướng chuyển động ban đầu của viên bi 1.

Chọn chiều dương là chiều chuyển động của bi 1, bi 2 ban đầu.

Ta có: \(m_{1} \text{v}_{1} + m_{2} \text{v}_{2} = \left(\right. m_{1} + m_{2} \left.\right) \text{v}\)

\(\Rightarrow \text{v}_{2} = \frac{\left(\right. m_{1} + m_{2} \left.\right) \text{v} - m_{1} \text{v}_{1}}{m_{2}} = \frac{\left(\right. 0 , 5 + 0 , 3 \left.\right) . 3 - 0 , 5.4}{0 , 3} = 1 , 33\) m/s

b. Sau va chạm chúng dính vào nhau và chuyển động động với vận tốc \(\text{v}\) = 3 m/s theo hướng vuông góc với hướng chuyển động ban đầu của viên bi 1.

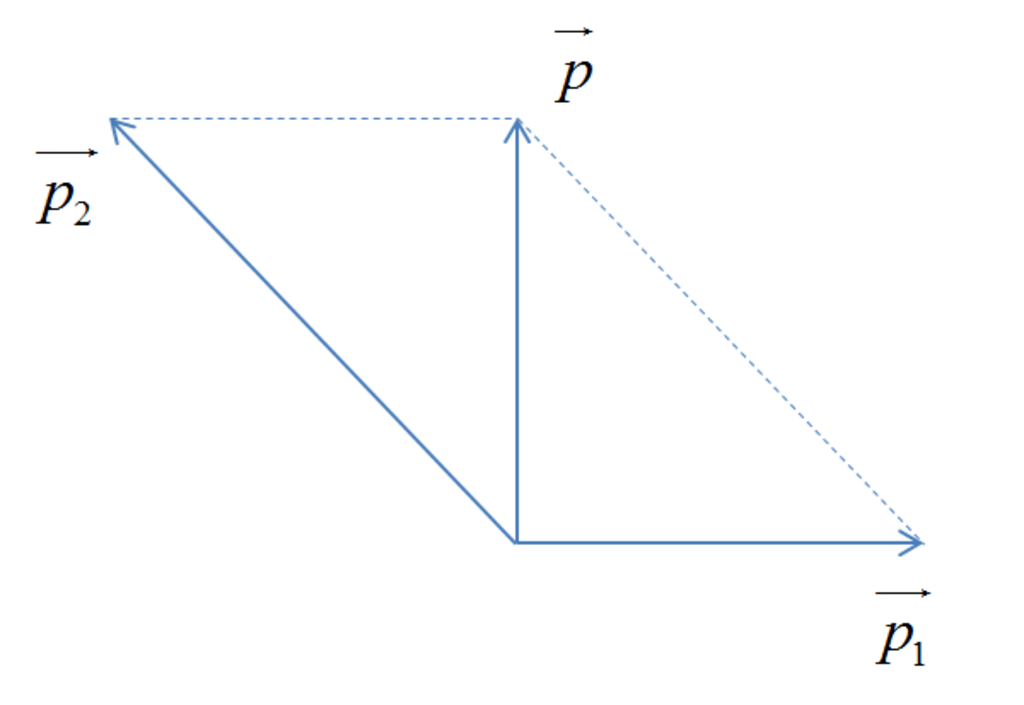
Từ hình vẽ ta suy ra: \(p_{2} = \sqrt{p^{2} + p_{1}^{2}}\)

\(p = \left(\right. m_{1} + m_{2} \left.\right) \text{v} = \left(\right. 0 , 5 + 0 , 3 \left.\right) . 3 = 2 , 4\) kg.m/s

\(p_{1} = m_{1} \text{v}_{1} = 0 , 5.4 = 2\) kg.m/s

\(\Rightarrow p_{2} = 3 , 12\) kg.m/s

\(\text{v}_{2} = \frac{p_{2}}{m_{2}} = \frac{3 , 12}{0 , 3} = 10 , 4\) m/s

- Tính đàn hồi: lò xo có khả năng biến dạng khi bị kéo hoặc nén và trở về hình dạng ban đầu khi lực tác dụng bị loại bỏ.

- Độ cứng: độ cứng \(k\) là một hằng số với lò xo xác định, phụ thuộc vào kích thước, hình dạng và vật liệu của lò xo. Trong hệ SI, \(k\) có đơn vị là N/m.

- Độ biến dạng: là độ dãn hoặc độ nén so với chiều dài tự nhiên của lò xo.

Ta có: \(\Delta l = l - l_{0}\)

Với \(\Delta l\) là độ biến dạng của lò xo (m); \(l\) là chiều dài của lò xo khi bị biến dạng (m); \(l_{0}\) là chiều dài tự nhiên của lò xo (m).

- Giới hạn đàn hồi: là độ biến dạng tối đa mà lò xo có thể chịu mà vẫn có thể trở về hình dạng ban đầu.

Một số giải pháp:

1. Gắn biển giới hạn tốc độ tại các khúc cua (đường cong)

·      Tình huống: Xe ô tô hoặc xe máy vào cua với tốc độ cao dễ bị văng ra khỏi quỹ đạo vì không đủ lực hướng tâm.

·      Giải pháp: Gắn biển báo tốc độ tối đa ở các khúc cua để tài xế giảm tốc → tránh trượt bánh hoặc lật xe.

2. Tăng độ nhám của mặt đường ở các đoạn cong

·      Tình huống: Trời mưa hoặc đường trơn làm giảm ma sát, không đủ lực ma sát để đóng vai trò lực hướng tâm, xe dễ trượt ra ngoài.

·      Giải pháp: Tráng nhựa chống trơn, dùng vật liệu tạo ma sát cao, khắc rãnh chống trượt → tăng lực ma sát giữa bánh xe và mặt đường → tăng lực hướng tâm.

3. Nghiêng mặt đường vào phía tâm cong

·      Tình huống: Khi xe vào khúc cua, lực quán tính làm xe có xu hướng lao ra ngoài.

·      Giải pháp: Thiết kế mặt đường nghiêng về phía trong khúc cua (nghiêng theo chiều cong) → tạo thành thành phần của phản lực pháp tuyến đóng vai trò là lực hướng tâm → giúp xe bám đường tốt hơn, giảm nguy cơ trượt hoặc lật.

4. Sử dụng dây an toàn và thanh chặn cơ thể trong các trò chơi mạo hiểm có chuyển động tròn

·      Tình huống: Khi người chơi chuyển động tròn (ví dụ: tàu lượn siêu tốc, đu quay), lực quán tính làm họ có xu hướng bị văng khỏi ghế.

·      Giải pháp: Trang bị dây an toàn, thanh chắn an toàn để giữ cơ thể cố định, chống lại lực quán tính (vốn làm người rời khỏi quỹ đạo tròn) → đảm bảo an toàn trong chuyển động.

5. Giảm khối lượng phương tiện hoặc tăng bán kính đường cong khi thiết kế

·      Tình huống: Để chuyển động tròn an toàn, lực hướng tâm phải đủ lớn, nhưng nếu xe quá nặng hoặc quỹ đạo cong quá gấp thì lực cần thiết rất lớn.

·      Giải pháp:

- Giảm khối lượng xe (nhẹ hơn → cần lực hướng tâm nhỏ hơn).

- Tăng bán kính cong của đường → giảm lực hướng tâm cần thiết.

a. Thí nghiệm va chạm đàn hồi:

Dùng hai xe A và B giống nhau, đầu mỗi xe có gắn một quả cầu kim loại nhỏ, cho xe A chuyển động với vận tốc \(v_{A} = v\) tới va chạm với xe B đang đứng yên. Kết quả va chạm làm xe A đang chuyển động thì dừng lại, còn xe B đang đứng yên thì chuyển động với đúng vận tốc \(v_{B}^{'} = v\).

b. Thí nghiệm va chạm mềm:

Dùng hai xe A và B giống nhau, ở đầu mỗi xe có gắn một miếng nhựa dính. Cho xe A chuyển động với vận tốc \(v_{A} = v\) tới va chạm với xe kia đang đứng yên. Sau va chạm, cả hai xe dính vào nhau và chuyển động với vận tốc \(v_{A B} = \frac{v}{2}\).

a. Độ biến dạng của lò xo là:

\(\Delta l = l - l_{0} = 23 - 20 = 3\) cm = 0,03 m

b. Khi vật ở trạng thái cân bằng, ta có: \(F_{đ h} = P\)

Theo Định luật Hooke: \(F_{đ h} = k . \Delta l\)

Trọng lực của vật: \(P = m g\)

Suy ra: \(k \Delta l = m g \Rightarrow k = \frac{m g}{\Delta l} = \frac{0 , 3.10}{0 , 03} = 100\) N/m

a. Điều kiện để một vật chuyển động tròn đều:

- Quỹ đạo chuyển động của vật là một đường tròn.

- Tốc độ dài của vật không đổi theo thời gian.

- Hợp lực tác dụng lên vật phải hướng vào tâm quỹ đạo của vật. Hợp lực này lực hướng tâm.

b. Các đặc điểm của lực hướng tâm:

- Phương: trùng với bán kính quỹ đạo.

- Chiều: hướng vào tâm của đường tròn.

- Độ lớn: \(F = \frac{m v^{2}}{r} = m \omega^{2} r\)

Trong đó: \(m\) là khối lượng của vật (kg); \(v\) là tốc độ dài (m/s); \(r\) là bán kính quỹ đạo (m); \(\omega\) là tốc độ góc (rad/s).

* Ví dụ về lực hướng tâm trong thực tế:

- Lực hấp dẫn giữ cho Trái Đất quay quanh Mặt Trời.

- Lực căng dây khi quay một vật buộc vào dây theo quỹ đạo tròn.

- Lực ma sát giữa lốp xe và mặt đường khi xe vào cua.

a. Gọi \(\left(\overset{\rightarrow}{p}\right)_{1}\) và \(\left(\overset{\rightarrow}{p}\right)_{1}^{^{'}}\) lần lượt là động lượng của vật 1 trước và sau khi xảy ra tương tác.

Gọi \(\left(\overset{\rightarrow}{p}\right)_{2}\) và \(\left(\overset{\rightarrow}{p}\right)_{2}^{^{'}}\) lần lượt là động lượng của vật 2 trước và sau khi xảy ra tương tác.

Định luật bảo toàn động lượng: động lượng của một hệ kín luôn bảo toàn, nghĩa là động lượng của từng vật trong hệ có thể thay đổi, nhưng tổng động lượng của các vật trong hệ không đổi.

Ta có: \(\overset{\rightarrow}{p} = \left(\overset{\rightarrow}{p}\right)_{1} + \left(\overset{\rightarrow}{p}\right)_{2} = \left(\overset{\rightarrow}{p}\right)_{1}^{^{'}} +\) \(\left(\overset{\rightarrow}{p}\right)_{2}^{^{'}}\)

b. - Va chạm đàn hồi là va chạm trong đó vật xuất hiện biến dạng đàn hồi trong khoảng thời gian va chạm. Sau va chạm, vật lấy lại hình dạng ban đầu và tiếp tục chuyển động tách rời nhau.

Trong va chạm đàn hồi, cả động lượng và động năng của hệ đều được bảo toàn.

- Va chạm mềm (hay va chạm không đàn hồi) xảy ra khi hai vật dính vào nhau và chuyển động với cùng vận tốc sau va chạm.

Trong va chạm mềm, động lượng của hệ được bảo toàn, động năng của hệ sau va chạm nhỏ hơn động năng của hệ trước va chạm.

Công có ích để nâng vật lên độ cao 10 m là

\(A_{1} = 10 m h = 10.200.10 = 20000\) J

Khi dùng hệ thống ròng rọc trên thì để vật lên được độ cao \(h\) ta phải kéo dây một đoạn \(S = 2 h\). Do đó, công dùng để kéo vật là

\(A = F_{1} . S = F_{1} . 2 h = 1500.2.10 = 30000\) J

Hiệu suất của hệ thống là

\(H = \frac{A_{1}}{A} . 100 \% = \frac{20000}{30000} . 100 \% \approx 66 , 67 \%\)

Chọn mốc thế năng tại mặt đất.

Theo định luật bảo toàn năng lượng

\(W = W_{d} + W_{t} = \frac{5}{2} W_{t} \rightarrow W = \frac{5}{2} m g h\)

\(\rightarrow m = \frac{2 W}{5 g h} = \frac{2.37 , 5}{5.10.3} = 0 , 5\) kg

Ta có:

\(W_{d} = \frac{3}{2} W_{t} \rightarrow \frac{1}{2} m v^{2} = \frac{3}{2} m g h \rightarrow v = \sqrt{3 g h} \approx 9 , 49\) m/s

Công của lực kéo là

\(A = F . s . c o s \alpha = 200.10. c o s 6 0^{o} = 1000\) J

Công suất của người đó là

\(P = \frac{A}{t} = \frac{1000}{5} = 200\) W