o \(A\) là trung điểm \(O B\), nên \(O B = 2. O A\).

Thay số \(O A = 2\) cm, ta có

\(O B = 2.2 = 4\) (cm)

2. (Không yêu cầu vẽ lại hình).

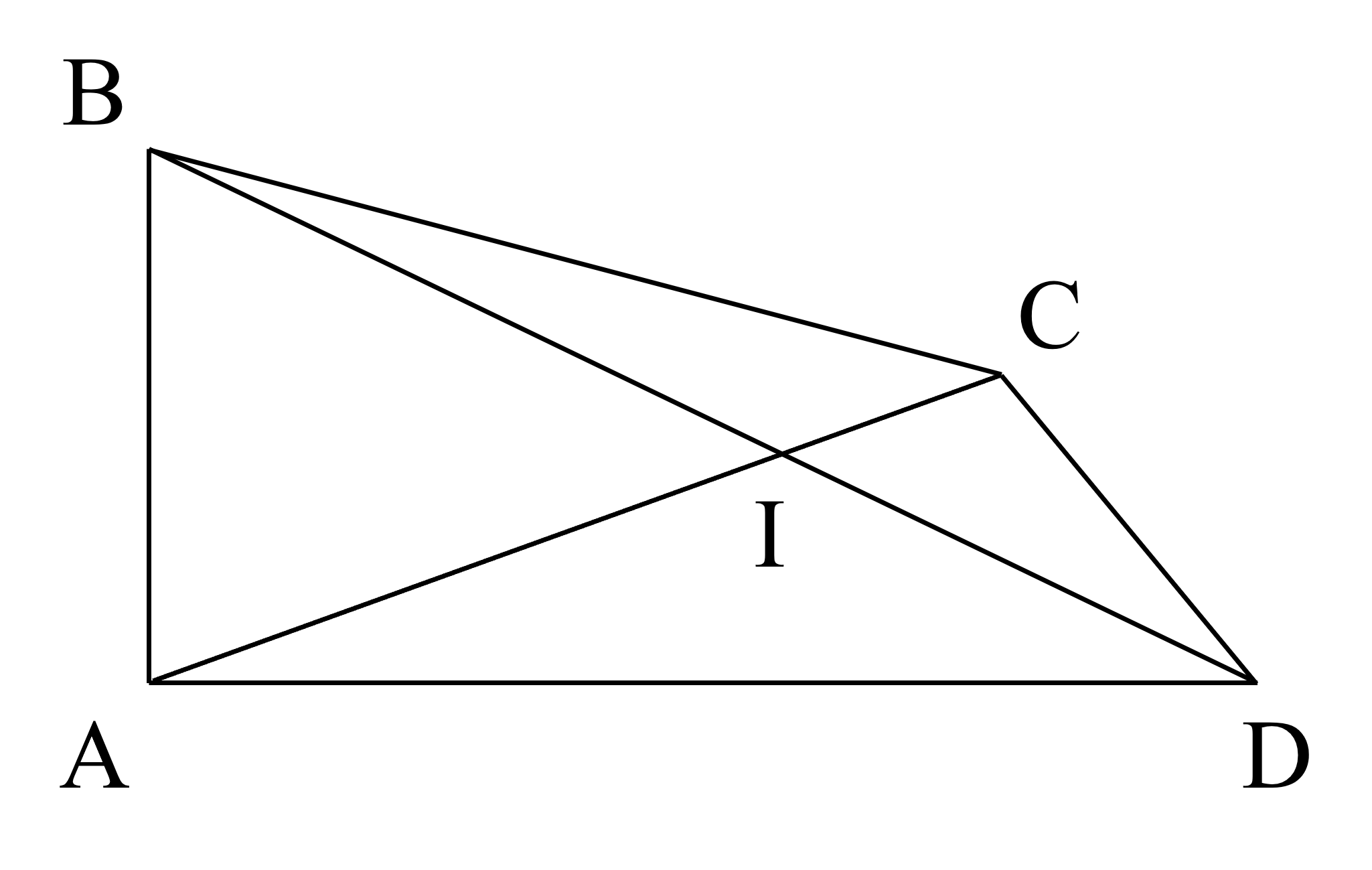
a) Điểm \(C\) và điểm \(I\) nằm trong góc \(B A D\).

b) (Học sinh nêu ra một góc bẹt sẽ đạt điểm tối đa phần này.)

Các góc bẹt trong hình là góc \(B I D\) và \(A I C\).

c) (Không trừ điểm học sinh khi đo góc có sai số từ \(1^{\circ}\) đến \(2^{\circ}\)).

Đo góc, ta lần lượt có các số đo góc như sau:

\(\hat{A I C} = 18 0^{\circ}\)

\(\hat{A C D} = 7 0^{\circ}\)

\(\hat{B C D} = 13 5^{\circ}\)

\(\hat{B A D} = 9 0^{\circ}\)

Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:

\(\hat{A C D} ; \hat{B A D} ; \hat{B C D} ; \hat{A I C}\).

Số học sinh đạt loại Tốt là:

\(45. \frac{4}{15} = 12\) (học sinh)

Số học sinh đạt loại Khá là:

\(12. \frac{5}{3} = 20\) (học sinh)

Số học sinh được xếp loại Đạt là:

\(45 - 12 - 20 = 13\) (học sinh)

Đáp số: \(13\) học sinh

a) \(\frac{1}{2} - \frac{1}{2} : x = \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{1}{2} - \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{- 1}{4}\)

\(x=\frac{1}{2}*\frac{- 1}{4}\)

\(x = - 2\)

b) \(\frac{x - 1}{15} = \frac{3}{5}\)

\(\frac{x - 1}{15} = \frac{9}{15}\)

\(x - 1 = 9\)

\(x = 10\)

c) \(x + 2 , 5 = 1 , 4\)

\(x = 1 , 4 - 2 , 5\)

\(x = - 1 , 1\)

A=(2,34+7,66)+(5,35+4,65)

=10+10

= 20

B=2,13.75+2,13.25

\(= 2 , 13. \left(\right. 75 + 25 \left.\right)\)

\(=2,13.100=213\)

c) \(C = \frac{1}{3} - \frac{1}{3} : \frac{3}{4}\)

\(=\frac{1}{3}-\frac{1}{3}*\frac{4}{3}\)

\(= \frac{1}{3} - \frac{4}{9}\)

\(= \frac{3}{9} - \frac{4}{9}\)

\(= \frac{- 1}{9}\) \(\)

1−21​+31​=66−3+2​=65​.

b) \(\frac{2}{5}+\frac{3}{5}:\frac{9}{10}=\frac{2}{5}+\frac{3}{5}\cdot\frac{10}{9}=\frac{2}{5}+\frac{2}{3}=\frac{14}{17}\).

c) \(\frac{7}{11} \cdot \frac{3}{4} + \frac{7}{11} \cdot \frac{1}{4} + \frac{4}{11} = \frac{7}{11} \left(\right. \frac{3}{4} + \frac{1}{4} \left.\right) + \frac{4}{11} = \frac{7}{11} + \frac{4}{11} = 1\).

d) \(\left(\right. \frac{3}{4} + 0 , 5 + 25 \% \left.\right) \cdot 2 \frac{2}{3} = \left(\right. \frac{3}{4} + \frac{1}{2} + \frac{1}{4} \left.\right) \cdot \frac{8}{3} = \frac{3}{2} \cdot \frac{8}{3} = 4\).

Các tia chung gốc \(A\) là:

   \(A B\) (hay \(A y\)); \(A M\) (hay \(A C\), \(A z\)); \(A x\).

Các điểm thuộc tia \(A z\) mà không thuộc tia \(A y\) là:

   \(M\) và \(C\).

Tia \(A M\) và tia \(M A\) không chung gốc nên không phải hai tia đối nhau.

Các tia chung gốc \(A\) là:

   \(A B\) (hay \(A y\)); \(A M\) (hay \(A C\), \(A z\)); \(A x\).

Các điểm thuộc tia \(A z\) mà không thuộc tia \(A y\) là:

   \(M\) và \(C\).

Tia \(A M\) và tia \(M A\) không chung gốc nên không phải hai tia đối nhau.