Chiều cao của mỗi hình chóp tứ giác đều là:

     \(30 : 2 = 15\) (m).

Thể tích của lồng đèn quả trám là:

     \(V=2(\frac13.20.20.15\left.\right)=4000\) (cm3).

Có \(19\) kết quả cho hành động trên.

Có \(8\) kết quả thuận lợi cho biến cố đã cho nên xác suất cho biến cố là: \(\frac{8}{19}\).

a) Xét đường thẳng: \(\left(\right. d_{1} \left.\right) : y = - 3 x\).

Nếu \(x = 0\) thì \(y = 0\) suy ra \(\left(\right. d_{1} \left.\right)\) đi qua điểm có tọa độ \(\left(\right. 0 ; 0 \left.\right)\)

Nếu \(x = 1\) thì \(y = - 3\) suy ra \(\left(\right. d_{1} \left.\right)\) đi qua điểm có tọa độ \(\left(\right. 1 ; - 3 \left.\right)\)

Ta vẽ đồ thị:

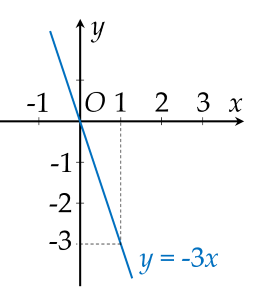
b) Vì \(\left(\right. d_{3} \left.\right) : y = a x + b\) song song với \(\left(\right. d_{2} \left.\right) : y = x + 2\) nên \(a = 1 , b \neq 2\).

Khi đó đường thẳng \(\left(\right. d_{3} \left.\right)\) có dạng \(y = x + b\) với \(b \neq 2\).

Vì \(\left(\right. d_{3} \left.\right)\) đi qua điểm có tọa độ \(A \left(\right. - 1 ; 3 \left.\right)\) nên: \(3 = - 1 + b\) hay \(b = 3 + 1 = 4\) (thỏa mãn).

Vậy đường thẳng \(\left(\right. d_{3} \left.\right)\) là \(\left(\right. d_{3} \left.\right) : y = - x + 4\).

2) Gọi số sản phẩm mà tổ I làm được theo kế hoạch là \(x\).

Điều kiện: \(x \in \mathbb{N}^{*}\); \(x < 900\), đơn vị: sản phẩm.

Số sản phẩm mà tổ II làm được theo kế hoạch là: \(900 - x\) (sản phẩm).

Theo bài ra, do cải tiến kĩ thuật nên tổ một vượt mức \(20 \%\) và tổ hai vượt mức \(15 \%\) so với kế hoạch.

Số sản phẩm mà tổ I làm được theo thực tế là: \(x + x . \&\text{nbsp}; 20 \% = x + 0 , 2 x = 1 , 2 x\) (sản phẩm);

Số sản phẩm mà tổ II làm được theo thực tế là: \(900 - x + \left(\right. 900 - x \left.\right) . 15 \% = 1 035 - 1 , 15 x\) (sản phẩm).

Vì thực tế hai tổ đã sản xuất được \(1 055\) sản phẩm nên ta có phương trình: \(1 , 2 x + 1 035 - 1 , 15 x = 1 055\)

Giải phương trình tìm được \(x = 400\) (sản phẩm)

Khi đó, số sản phẩm mà tổ II làm được theo kế hoạch là: \(900 - 400 = 500\) (sản phẩm).

Vậy theo kế hoạch tổ I làm được \(400\) sản phẩm, tổ II làm được \(500\) sản phẩm.

a, phương trình có nghiệm là x = 7

b, phương trình có nghiệm là x = 94/13