a) Chiều rộng của thửa rộng là:

\(20. \frac{9}{10} = 18\) (m)

Diện tích của thửa rộng là:

\(20.18 = 360\) (m\(^{2}\))

b) Số kg thóc mà thửa ruộng thu hoạch được là:

\(0 , 75.360 = 270\) (kg).

Số kg gạo mà thửa ruộng thu hoạch được là:

\(270.70 \% = 189\) (kg).

15.3=45 (học sinh)

c) Số học sinh đi bộ là:

\(3.3 = 9\) (học sinh)

Tỉ số phần trăm học sinh đi bộ đến trường là:

\(9 : 45 = \frac{1}{5} = 20 \%\)

a) \(A = \frac{- 3}{4} - \frac{1}{3}\)

\(= \frac{- 9}{12} - \frac{4}{12}\)

\(= \frac{- 9}{12} + \frac{- 4}{12}\)

\(= \frac{- 9 - 4}{12}\)

\(= \frac{- 13}{12}\)

b) \(B = 26 , 8 - 6 , 8.4\)

\(= 26 , 8 - 27 , 2\)

\(= - 0 , 4\)

c) \(\frac{1}{3} + \frac{2}{3} : x = \frac{- 1}{2}\)

\(\frac{2}{3} : x = \frac{- 1}{2} - \frac{1}{3}\)

\(\frac{2}{3} : x = - \frac{5}{6}\)

\(x = \frac{2}{3} : \left(\right. - \frac{5}{6} \left.\right)\)

\(x = - \frac{4}{5}\)

d) Số tiền được giảm giá là:

\(50\) \(000.\) \(10 \% =\) \(50\) \(000.\) \(\frac{10}{100}\) \(= 5000\) (đồng)

Số tiền Nam phải trả là:

\(50\) \(000 -\) \(5\) \(000\) \(= 45\) \(000\) (đồng)

Đáp số: \(45\) \(000\) đồng.

a) \(\frac{6}{5} + \frac{4}{3} . \frac{21}{8} - \frac{13}{10} = \frac{6}{5} + \frac{7}{2} - \frac{13}{10} = \frac{12}{10} + \frac{35}{10} - \frac{13}{10} = \frac{34}{10} = \frac{17}{5}\).

b) \(\frac{- 11}{12} . \frac{18}{25} + \frac{- 11}{12} . \frac{7}{25} + \frac{11}{12} = \frac{- 11}{12} . \left(\right. \frac{18}{25} + \frac{7}{25} - 1 \left.\right) = \frac{- 11}{12} . 0 = 0\).

c) \(12 , 89 - 43 , 65 + 27 , 11 + \left(\right. - 56 , 35 \left.\right)\) 

 \(= \left(\right. 12 , 89 + 27 , 11 \left.\right) - \left(\right. 43 , 65 + 56 , 35 \left.\right)\)

 \(= 40 - 100 = - 60.\)

d) \(1 \frac{13}{15} . \left(\left(\right. 0 , 5 \left.\right)\right)^{2} . 3 + \left(\right. \frac{8}{15} - 1 \frac{19}{60} \left.\right) : 1 \frac{23}{24}\)

 \(= \frac{28}{15} . \frac{1}{4} . 3 + \left(\right. \frac{8}{15} - \frac{79}{60} \left.\right) : \frac{47}{24}\)

 \(= \frac{7}{5} + \left(\right. \frac{- 47}{60} \left.\right) : \frac{47}{24}\)

 \(= \frac{7}{5} + \left(\right. \frac{- 2}{5} \left.\right)\)

 \(= 1\).

Gọi \(d =\) ƯCLN\(\left(\right. 14 n + 3 , 21 n + 4 \left.\right)\).

Có \(14 n + 3\) chia hết cho d và \(21 n + \&\text{nbsp}; 4\) chia hết cho \(d\).

Từ đó suy ra: \(3. \left(\right. 14 n + 3 \left.\right) - 2. \left(\right. 21 n + 4 \left.\right) = 1\) chia hết cho \(d\).

Vậy \(d = \&\text{nbsp}; 1\) hay \(\frac{14 n + 3}{21 n + 4}\) là phân số tối giản.

a) Ngày thứ nhất, bạn Hạnh đọc số trang sách là:

\(240. \frac{3}{5} = 144\) (trang)

b) Ngày thứ hai, bạn Hạnh đọc số trang sách là:

\(240 - 144 = 96\) (trang)

Số trang sách bạn Hạnh đọc trong ngày thứ hai chiếm số phần trăm số trang sách của cuốn sách là:

\(\frac{96}{240} . 100 \% = 40 \%\).

Gọi \(d =\) ƯCLN\(\left(\right. 14 n + 3 , 21 n + 4 \left.\right)\).

Có \(14 n + 3\) chia hết cho d và \(21 n + \&\text{nbsp}; 4\) chia hết cho \(d\).

Từ đó suy ra: \(3. \left(\right. 14 n + 3 \left.\right) - 2. \left(\right. 21 n + 4 \left.\right) = 1\) chia hết cho \(d\).

Vậy \(d = \&\text{nbsp}; 1\) hay \(\frac{14 n + 3}{21 n + 4}\) là phân số tối giản.

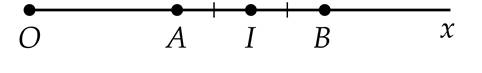
a) Vì điểm \(A \&\text{nbsp};\)và điểm \(B\) đều nằm trên tia \(O x\) nên \(A\) và \(B\) nằm cùng phía so với điểm \(O\)

\(A B = O B - O A = 6 - 3 = 3\) (cm)

b) Vì \(O A = A B = 3\) cm và \(A\) nằm giữa \(O\) và \(B\).

Nên \(A\) là trung điểm của \(O B\).

c) Vì \(I\) là trung điểm \(A B\) nên\(A I = I B = \frac{1}{2} . 3 = \frac{3}{2} \&\text{nbsp};\)(cm)

\(O I = O A + A I = 3 + \frac{3}{2} = \frac{9}{2} \&\text{nbsp};\)(cm).

Gọi \(d =\) ƯCLN\(\left(\right. 14 n + 3 , 21 n + 4 \left.\right)\).

Có \(14 n + 3\) chia hết cho d và \(21 n + \&\text{nbsp}; 4\) chia hết cho \(d\).

Từ đó suy ra: \(3. \left(\right. 14 n + 3 \left.\right) - 2. \left(\right. 21 n + 4 \left.\right) = 1\) chia hết cho \(d\).

Vậy \(d = \&\text{nbsp}; 1\) hay \(\frac{14 n + 3}{21 n + 4}\) là phân số tối giản.

Gọi \(d =\) ƯCLN\(\left(\right. 14 n + 3 , 21 n + 4 \left.\right)\).

Có \(14 n + 3\) chia hết cho d và \(21 n + \&\text{nbsp}; 4\) chia hết cho \(d\).

Từ đó suy ra: \(3. \left(\right. 14 n + 3 \left.\right) - 2. \left(\right. 21 n + 4 \left.\right) = 1\) chia hết cho \(d\).

Vậy \(d = \&\text{nbsp}; 1\) hay \(\frac{14 n + 3}{21 n + 4}\) là phân số tối giản.