Bài 4:

Kích thước: \(x\), \(x + 1\), \(x - 1\)

a)
Thể tích:
\(V = x \left(\right. x + 1 \left.\right) \left(\right. x - 1 \left.\right)\)
\(= x \left(\right. x^{2} - 1 \left.\right) = x^{3} - x\)
→ \(\boxed{x^{3} - x}\)

b)
Thay \(x = 4\):
\(V = 4^{3} - 4 = 64 - 4 = \boxed{60}\)

Bài 3:

Chia đa thức:
\(A = 2 x^{4} - 3 x^{3} - 3 x^{2} + 6 x - 2\)
\(B = x^{2} - 2\)

Đặt tính chia:

→ Thương: \(\boxed{2 x^{2} - 3 x + 1}\), dư: \(\boxed{0}\)

Bài 2:

5

𝑥

(

4

𝑥

2

−

2

𝑥

+

1

)

−

2

𝑥

(

10

𝑥

2

−

5

𝑥

+

2

)

=

−

36

5x(4x

2

−2x+1)−2x(10x

2

−5x+2)=−36

=

20

𝑥

3

−

10

𝑥

2

+

5

𝑥

−

20

𝑥

3

+

10

𝑥

2

−

4

𝑥

=20x

3

−10x

2

+5x−20x

3

+10x

2

−4x

=

𝑥

=x

𝑥

=

−

36

x=−36

→

𝑥

=

−

36

x=−36

​

:\(\boxed{0}\)

Bài 1:

a)
\(P \left(\right. x \left.\right) + Q \left(\right. x \left.\right) = \left(\right. x^{4} - 5 x^{3} + 4 x - 5 \left.\right) + \left(\right. - x^{4} + 3 x^{2} + 2 x + 1 \left.\right)\)
\(= 0 x^{4} - 5 x^{3} + 3 x^{2} + 6 x - 4\)
→ \(\boxed{- 5 x^{3} + 3 x^{2} + 6 x - 4}\)

b)
\(R \left(\right. x \left.\right) = P \left(\right. x \left.\right) - Q \left(\right. x \left.\right)\)
\(= \left(\right. x^{4} - 5 x^{3} + 4 x - 5 \left.\right) - \left(\right. - x^{4} + 3 x^{2} + 2 x + 1 \left.\right)\)
\(= x^{4} + x^{4} - 5 x^{3} - 3 x^{2} + 4 x - 2 x - 5 - 1\)
\(= 2 x^{4} - 5 x^{3} - 3 x^{2} + 2 x - 6\)
→ \(\boxed{2 x^{4} - 5 x^{3} - 3 x^{2} + 2 x - 6}\)

Câu a: Chứng minh $△BAD=△BFD$

Phân tích đề bài:

• $△ABC$ cân tại $A$ $\Rightarrow AB=AC$.

• $BD$ là phân giác của $\angle B$ $\Rightarrow$ chia $△ABC$ thành hai phần.

• $△BAF$ cân tại $B$ $\Rightarrow BF=BA$.

• $△BDE$ cân tại $B$ $\Rightarrow BD=BE$.

Chứng minh:

Xét hai tam giác $△BAD$ và $△BFD$:

1. $AB=BF$ (do $△BAF$ cân tại $B$).

2. $BD$ chung.

3. $\angle ABD=\angle FBD$ (vì $BD$ là phân giác của $\angle B$).

Từ ba yếu tố trên, theo trường hợp cạnh - góc - cạnh (c-g-c), ta có:

$$△BAD=△BFD.$$

Câu b: Chứng minh $△DEF$ cân

Chứng minh:

Xét $△DEF$:

• Đã biết $△BDE$ cân tại $B$ $\Rightarrow BD=BE$.

• Đã chứng minh $△BAD=△BFD$, nên $AD=DF$.

• Vì $BD=BE$ và $△BDE$ cân tại $B$, ta suy ra $DE=DF$.

Vậy $△DEF$ là tam giác cân tại $D$.

Bước 1: Gọi số máy của từng đội

Gọi:

• $x$ là số máy của đội thứ nhất.

• $y$ là số máy của đội thứ hai.

• $z$ là số máy của đội thứ ba.

Theo đề bài, ta có:

$$y=z+5$$

Bước 2: Biểu diễn năng suất làm việc

Gọi năng suất của một máy là $a$ (cày được bao nhiêu phần cánh đồng trong một ngày).

• Đội thứ nhất cày xong trong 5 ngày, nên tổng năng suất của đội là $5xa=1$ (hoàn thành toàn bộ cánh đồng).

  $$5xa=1$$ xa=15xa = \frac{1}{5}xa=51​

• Đội thứ hai cày xong trong 6 ngày, nên:

  $$6ya=1$$ ya=16ya = \frac{1}{6}ya=61​

• Đội thứ ba cày xong trong 8 ngày, nên:

  $$8za=1$$ za=18za = \frac{1}{8}za=81​

Bước 3: Lập hệ phương trình

Ta có:

xa=15,ya=16,za=18x a = \frac{1}{5}, \quad y a = \frac{1}{6}, \quad z a = \frac{1}{8}xa=51​,ya=61​,za=81​

Chia từng vế cho $a$, ta có:

x=15a,y=16a,z=18ax = \frac{1}{5a}, \quad y = \frac{1}{6a}, \quad z = \frac{1}{8a}x=5a1​,y=6a1​,z=8a1​

Từ phương trình $y=z+5$, thay vào:

16a=18a+5\frac{1}{6a} = \frac{1}{8a} + 56a1​=8a1​+5

Nhân cả hai vế với $24a$ để khử mẫu:

$$4=3+120a$$ $$1=120a$$ a=1120a = \frac{1}{120}a=1201​

Bước 4: Tính số máy của từng đội

x=15a=15×1120=1205=24x = \frac{1}{5a} = \frac{1}{5 \times \frac{1}{120}} = \frac{120}{5} = 24x=5a1​=5×1201​1​=5120​=24 y=16a=16×1120=1206=20y = \frac{1}{6a} = \frac{1}{6 \times \frac{1}{120}} = \frac{120}{6} = 20y=6a1​=6×1201​1​=6120​=20 z=18a=18×1120=1208=15z = \frac{1}{8a} = \frac{1}{8 \times \frac{1}{120}} = \frac{120}{8} = 15z=8a1​=8×1201​1​=8120​=15

Câu a: Tính $P(x)-Q(x)$

Ta có:

P(x)=x3−3x2+x+1P(x) = x^3 - 3x^2 + x + 1P(x)=x3−3x2+x+1 Q(x)=2x3−x2+3x−4Q(x) = 2x^3 - x^2 + 3x - 4Q(x)=2x3−x2+3x−4

Tính $P(x)-Q(x)$:

P(x)−Q(x)=(x3−3x2+x+1)−(2x3−x2+3x−4)P(x) - Q(x) = (x^3 - 3x^2 + x + 1) - (2x^3 - x^2 + 3x - 4)P(x)−Q(x)=(x3−3x2+x+1)−(2x3−x2+3x−4)

Phân phối dấu trừ:

P(x)−Q(x)=x3−3x2+x+1−2x3+x2−3x+4P(x) - Q(x) = x^3 - 3x^2 + x + 1 - 2x^3 + x^2 - 3x + 4P(x)−Q(x)=x3−3x2+x+1−2x3+x2−3x+4

Nhóm các hạng tử cùng bậc lại:

(x3−2x3)+(−3x2+x2)+(x−3x)+(1+4)(x^3 - 2x^3) + (-3x^2 + x^2) + (x - 3x) + (1 + 4)(x3−2x3)+(−3x2+x2)+(x−3x)+(1+4) −x3−2x2−2x+5- x^3 - 2x^2 - 2x + 5−x3−2x2−2x+5

Vậy:

P(x)−Q(x)=−x3−2x2−2x+5P(x) - Q(x) = -x^3 - 2x^2 - 2x + 5P(x)−Q(x)=−x3−2x2−2x+5

Câu b: Chứng minh $x=1$ là nghiệm của cả hai đa thức

Thay $x=1$ vào $P(x)$:

P(1)=13−3(12)+1+1P(1) = 1^3 - 3(1^2) + 1 + 1P(1)=13−3(12)+1+1 $$=1-3+1+1=0$$

Vậy $x=1$ là nghiệm của $P(x)$.

Thay $x=1$ vào $Q(x)$:

Q(1)=2(13)−(12)+3(1)−4Q(1) = 2(1^3) - (1^2) + 3(1) - 4Q(1)=2(13)−(12)+3(1)−4 $$=2-1+3-4=0$$

Vậy $x=1$ là nghiệm của $Q(x)$.

Kết luận: $x=1$ là nghiệm của cả hai đa thức $P(x)$ và $Q(x)$.

a)

x−4−4=−112\frac{x - 4}{-4} = \frac{-11}{2}−4x−4​=2−11​

Nhân chéo:

$$(x-4)\cdot 2=(-4)\cdot (-11)$$ $$2x-8=44$$ $$2x=52$$ $$x=26$$

b)

15−xx+9=35\frac{15 - x}{x + 9} = \frac{3}{5}x+915−x​=53​

Nhân chéo:

$$(15-x)\cdot 5=(x+9)\cdot 3$$ $$75-5x=3x+27$$ $$75-27=5x+3x$$ $$48=8x$$ $$x=6$$

Kết quả:

• a) $x=26$

• b) $x=6$

a có hình vẽ:

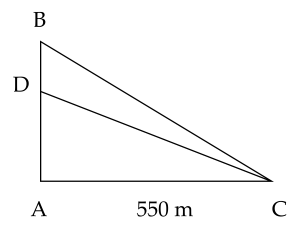
Gọi vị trí đặt loa là $D$ suy ra $D$ nằm giữa $A$ và $B$.Trong tam giác vuông $ADC$ ta có $DC$ là cạnh lớn nhất (đối diện với góc lớn nhất) nên $DC>AC=550$ m. Vậy tại $C$ không thể nghe tiếng loa, do vị trí $C$ đã nằm ngoài bán kính phát sóng của loa.